序論

みなさんこんにちは。 この記事は東京大学理学部物理学科(響きがカッコ良すぎる)の有志による企画「理物アドベントカレンダー」の一環として寄稿するものです。 他の方の記事はこちらから。 12/11の投稿枠を押さえたときは、京大生か東工大の批判記事でも書こうと意気込んでいたわけですが、その日が近づくにつれて僕の理性が敵愾心を抑圧して結局物理の話を書くことになりました。

経済物理学

とは何か、と聞かれるととても困ります。そういうときは 「為替レートの変動とかがブラウン運動とみなせて・・・」などと言うと大抵の人は納得してくれます。いかにも経済の対象らしい「為替レート」と高校の物理か化学で耳にした「ブラウン運動」が同一文中に並んでいるからです。しかし中にはめんどくせぇ鋭い方が居て、「ブラウン運動は確率過程を扱う数理モデルであって、物理とは独立なはず。為替レートがブラウン運動するからといって即ち物理につながるものでは無い。経済の中に勝手に物理を見出して気持ちよくなっているだけではないか」(意訳) などとのたまうわけです。真実はいつでも人を傷つけるもので、僕自身かなり思い悩みました。つまり、金融工学と経済物理学の違いを説明できなかったわけです。これは偏に僕の不勉強によるもので、今は自分の中で一応の答えを持っているつもりです。しかしそれは一言で表現できるものではないので、今回はその雰囲気ををみなさんにお伝えできれば著者としてこの上ない喜びです。

まずはじめの動機としては

価格変動を説明したい

というものがあります。為替レートを想定してみてください。チャートを観察しても特別な法則性は見えてきませんよね(少なくとも僕には)。でもそんな不規則なものを予測したいわけです。みなさんに少しでも金銭欲があればこのモチベーションは共有できるはずです。そして価格は時間の一価関数

\(\hspace{0.2em}f(t)\hspace{-0.2em}\hspace{0.2em}\) のように書けない(つまりそんなに単純じゃない)ことはわかると思います。では \(\hspace{-0.2em}\hspace{0.2em}f(t,x,y,z,…)\hspace{-0.2em}\hspace{0.2em}\) のように変数を増やせば良いかと言うと、それも現実的ではありません。そんなことをしてもいたずらに変数が増えるだけですし、それで説明できるようになる保証もありません。そのためふつう価格というものは非決定論的に扱います。つまり、初期条件を完全に揃えた状況をもう一度作り出して価格変化を見ても前回とは違う結果になる、という立場です。

Ising(イジング)モデル

一旦経済から離れて、物理のお話をしましょう。イジングモデルはシンプルなモデルながら物質の磁性とその温度依存性を良く説明するものです。 ハミルトニアン(耳慣れない方はエネルギーと読み換えてください)は

と書けて、第一項が隣接スピンの相互作用を、第二項が外場との相互作用を表します。\({J > 0}\hspace{0.2em}\)のとき、\({\sigma_i\sigma_j=-1}\)、すなわち隣り合うスピンが違う方向を向いた状態が第一項を最小にします。\({J < 0}\hspace{0.2em}\)なら反対に、すべてのスピンが揃った状態がスピン間相互作用を最小にします。一方\(\hspace{0.2em}{h}\hspace{0.2em}\)は外からかける磁場の向きを表していて\(\hspace{0.2em}{h < 0}\hspace{0.2em}\)ならすべてのスピンが上(\({\sigma_i=+1}\hspace{0.2em}\))のとき第二項は最小となります。vice versa。エネルギーが低い状態が実現しやすいということを念頭に置くと\(\hspace{0.2em}{J}\hspace{0.2em}\)によって磁性の違いが表現できることがわかります。ここで特筆すべきは、「磁性」というマクロに観測される量の振る舞いを説明するために「スピン」というミクロな、そして根源的なものを導入して議論をしている、ということです。これが統計力学というものなのですが、このような発想は意外と経済や金融工学では見られないのではないでしょうか。

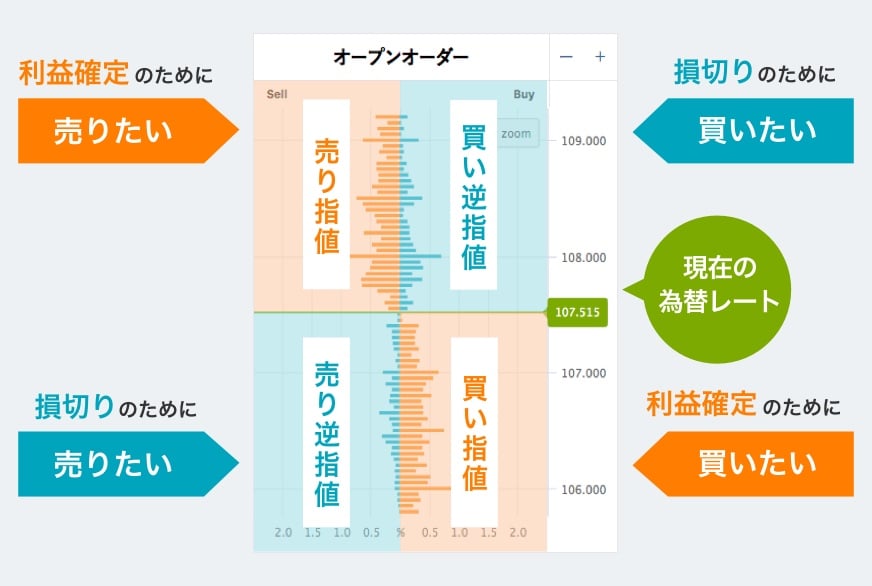
そこで各サイトを人に見立ててみようという発想が生まれます。つまり\(\hspace{0.2em}{i}\hspace{0.2em}\)番目の人が「今後価格が上がる」と思っているなら買い(\({\sigma_i=+1}\hspace{0.2em}\))、下がると思っているなら売り(\({\sigma_i=-1}\hspace{0.2em}\))といった具合です。市場参加者が相互作用しながら売りと買いが動き、やがて平衡状態に落ち着くでしょう。売りと買いの数はオーダーブックから知ることができます。もちろん時間とともに変化するわけですが、それは適当な時間スケールでは平衡状態まわりのゆらぎとして解釈します。

何やら良さげですが、少なくとも2つの問題があります。

IS モデル

まず1つに「サイトが固定されている」問題です。サイトは動かないけれど各サイトのスピンが変わりうる、としているわけです。イジングモデルは磁性体を背景としたモデルですから当然といえば当然ですね。ハミルトニアンを思い出すとサイト間の相互作用は隣接サイト間のみに限定されています。そのため\(\hspace{0.2em}{d}\hspace{0.2em}\)次元イジングモデルでは、サイト\(\hspace{0.2em}{i}\hspace{0.2em}\)にとって隣接する\(\hspace{0.2em}{2d}\hspace{0.2em}\)個のサイトが特別、と言うこともできるでしょう。物理の場合距離が離れれば影響力が急激に減衰する、ということがある程度正当化できますが、経済の場合はどうでしょう？市場参加者それぞれについて特別な\(\hspace{0.2em}{2d}\hspace{0.2em}\)人の特別な相手がいるとは思えません。むしろ全体の売り・買い比率に影響を受けるとした方が良さそうです。

問題がこれだけであれば相互作用の範囲を広げた、無限レンジイジングモデルで解決できそうですね。ですが「人は頑固」だということを忘れてはいけません。つまり人は自分と同じ意見を聞きたがるものです。イジングモデルではサイト\(\hspace{0.2em}{i}\hspace{0.2em}\)に隣接する\(\hspace{0.2em}{2d}\hspace{0.2em}\)個のサイトのスピンが\(\hspace{0.2em}{\sigma_i}\hspace{0.2em}\)と同符号でも異符号でも同じ大きさの影響をサイト\(\hspace{0.2em}{i}\hspace{0.2em}\)に与えます。それでは素直すぎるというわけです。そこで仮想的に同じ向きのスピンを一箇所に集めてみましょう。そうすれば上向きスピンと下向きスピンが触れ合う部分が少なくなりますね。この触れ合う部分を最小にするには、上向きスピンと下向きスピンのうち数が少ない方を\(\hspace{0.2em}{d}\hspace{0.2em}\)次元座標の中心に寄せて球にしてしまえば良いでしょう。(実際にサイトを動かすわけでは無いことに注意)

平均場\(\hspace{0.2em}{m:=\sum_i\sigma_i/N}\hspace{0.2em}\)を導入すると、上向きスピンと下向きスピンの数はそれぞれ

と書ける。このうち小さい方は

と書けて、異なる向きのスピンが触れ合う部分は\(\hspace{0.2em}{N'^{1-1/d}}\hspace{0.2em}\)に比例するでしょう。 これがISモデルのハミルトニアンです(なんでISモデルと言うのか、明日までに考えておいてください)。かなりごちゃごちゃした見た目なので難しそうですが、スピンはすべて平均場の形で入っているので、平均場近似(もはや近似でもない)と相性が良さそうです。今回は分配関数ではなくヘルムホルツ自由エネルギーを求めてしまった方が見通しが良いです。計算は割愛して自由エネルギー極小の条件から

という自己無撞着方程式が得られます。(経済物理ゼミのメンバーのアイデアを大いに参考にしました）

このモデルでは買いと売りがどれだけ強気なのかという要素を入れていませんが、\({m,N}\hspace{0.2em}\)はオーダーブックなどから観測可能な量です。\({J}\hspace{-0.2em}\hspace{0.2em}\) や\(\hspace{0.2em}{d}\hspace{0.2em}\)は市場固有のものと考えられるので、\({h}\hspace{0.2em}\)が定数とみなせる短時間領域でのゆらぎを予想するのに役立つであろうモデルです。

最後に

時間の都合上省略してしまった記述も多く、わかりにくい部分があったかもしれません。ですがこれをきっかけに経済物理に興味を持ってくれたならぜひPhysics Lab. 2023経済物理班にお越しください！余談ですが、このISモデルのハミルトニアンを経済物理ゼミで発表したとき、参加者が自由エネルギーから自己無撞着方程式まで導いてくれ、とても嬉しかった記憶があります。この瞬間、自分が作ったモデルを解くのに東京大学理学部物理学科の頭脳が向けられている、という事実が。Isingさんもこんな気持ちだったんですかね。では。