ベイズ推測と特異点解消

簡単な紹介

⚠記事の内容は学生個人の見解であり、所属する学科組織を代表するものではありません。

Twitterで共有

Physics Lab. 2022 Advent Calendar 22日目ベイズ推測と特異点解消

こんにちは！！理物3年のtgysです．

今日は12/22，冬至です．魔術師ラマヌジャンやフォック空間のフォックの誕生日でもあるみたいです．何の記事を書くか決めないまま当日を迎えてしまいました．

とりあえず最近自主ゼミ『ベイズ統計の理論と方法』で担当したベイズ推測への特異点解消の利用について書きます．

ある日突然この記事の内容がガラッと変わっていたら，それはきっと私がもっといい記事を思いついたということです．

ベイズ推測をざっとみる

此頃都ニハヤル物といえば，機械学習や深層学習ですね！理物でも4年生向けに機械学習の講義があるみたいです．

こうした「学習」のうち，ある種のものは，「サンプルデータを参考に、モデルを真の分布に近づける」ことに帰結します．ちょっと数学風に書き直してみましょう．

関数 $\hspace{-0.2em}\hspace{0.2em}q\colon\mathbb{R}^N\to\mathbb{R}_0^+\hspace{-0.2em}\hspace{0.2em}$ が

$$ \begin{align*}\int\mathrm{d}x\, q(x) = 1 \end{align*} $$

を満たすとき，確率分布とよびます．同じ確率分布 $\hspace{-0.2em}\hspace{0.2em}q(x)\hspace{-0.2em}\hspace{0.2em}$ にしたがう $\hspace{-0.2em}\hspace{0.2em}n\hspace{-0.2em}\hspace{0.2em}$ 個の独立な確率変数 $\hspace{-0.2em}\hspace{0.2em}X^n\coloneqq(X_1, X_2, \dots, X_n)\hspace{-0.2em}\hspace{0.2em}$ の実現値 $\hspace{-0.2em}\hspace{0.2em}x^n\coloneqq (x_1, x_2, \dots, x_n)\hspace{-0.2em}\hspace{0.2em}$ のことをサンプルとよび，そのときの $\hspace{-0.2em}\hspace{0.2em}q(x)\hspace{-0.2em}\hspace{0.2em}$ を特に真の分布といいます．今やりたいのは，確率変数 $\hspace{-0.2em}\hspace{0.2em}X^n\hspace{-0.2em}\hspace{0.2em}$ による，真の分布 $\hspace{-0.2em}\hspace{0.2em}q(x)\hspace{-0.2em}\hspace{0.2em}$ の推定です．

ベイズ推測

ベイズ推測では，パラメータ $\hspace{-0.2em}\hspace{0.2em}w\in W\subset \mathbb{R}^d\hspace{-0.2em}\hspace{0.2em}$ によって定まる確率モデル $\hspace{-0.2em}\hspace{0.2em}p_w(x)\hspace{-0.2em}\hspace{0.2em}$ とパラメータの分布：事前分布 $\hspace{-0.2em}\hspace{0.2em}\varphi(w)\hspace{-0.2em}\hspace{0.2em}$ をもちいます．これらを用いて，パラメータの新たな分布：事後分布 $\hspace{-0.2em}\hspace{0.2em}p_\mathrm{post}(w|X^n)\hspace{-0.2em}\hspace{0.2em}$ を

$$ p_\mathrm{post}(w|X^n)\coloneqq\cfrac{1}{Z_n(\beta)}\,\varphi(w)\prod_{i=1}^n p_w(X_i) $$

と定義します．ただし，規格化のための分配関数 $\hspace{-0.2em}\hspace{0.2em}Z(X^n)\hspace{-0.2em}\hspace{0.2em}$ を

$$ Z(X^n)\coloneqq\int_W\mathrm{d}w\,\varphi(w)\prod_{i=1}^n p_w(X_i) $$

とおきました，この定義は，サンプルによってパラメータ $\hspace{-0.2em}\hspace{0.2em}w\hspace{-0.2em}\hspace{0.2em}$ の分布を事前分布から事後分布に“修正”していることにあたります．事後分布によって確率モデルを平均した予測分布 $\hspace{-0.2em}\hspace{0.2em}p_\mathrm{pred}(x|X^n)\hspace{0.2em}$

$$ \begin{aligned} p_\mathrm{pred}(x|X^n)&\coloneqq\mathbb{E}_w[p_w(x)]\\ &=\int_W\mathrm{d}w\,p_w(x)\,p_\mathrm{post}(w|X^n) \end{aligned} $$

こそ，真の分布に近いと推測するのがベイズ推測です．

KL divergence

さて，ここまで漠然と「近さ」という言葉を使っていました．一般の確率分布間の「近さ」にあたるのが、Kullback–Leibler divergence (KL divergence)

$$ D_\mathrm{KL}[q_1(x), q_2(x)]\coloneqq \int\mathrm{d}x\, q_1(x)\log{\cfrac{q_1(x)}{q_2(x)}} $$

です．このとき，次の2つが成り立ちます．

任意の確率分布 $\hspace{-0.2em}\hspace{0.2em}q_1, q_2\hspace{-0.2em}\hspace{0.2em}$ について $\hspace{-0.2em}\hspace{0.2em}D_\mathrm{KL}[q_1(x), q_2(x)]\geq0\hspace{0.2em}$
$\hspace{-0.2em}D_\mathrm{KL}[q_1(x), q_2(x)]=0\hspace{0.5cm}\Longleftrightarrow\hspace{0.5cm}\hspace{0.2em}$任意の $\hspace{-0.2em}\hspace{0.2em}x\hspace{-0.2em}\hspace{0.2em}$ について $\hspace{-0.2em}\hspace{0.2em}q_1(x)=q_2(x)\hspace{0.2em}$

2つの確率分布が完全に一致したときのみ $\hspace{-0.2em}\hspace{0.2em}0\hspace{-0.2em}\hspace{0.2em}$ を返し，その他のときは正の実数を返すということです．「近さ」をはかるには嬉しい性質ですね！対称性はないことに注意しましょう．

平均対数損失関数と経験対数損失関数

平均対数損失関数 $\hspace{-0.2em}\hspace{0.2em}L(w)\hspace{-0.2em}\hspace{0.2em}$ を

$$ L(w)\coloneqq-\int\mathrm{d}x\,q(x)\log{p_w(x)}=-\int\mathrm{d}x\,q(x)\log{q(x)}+\int\mathrm{d}x\,q(x)\log{\cfrac{q(x)}{p_w(x)}}=S[q(x)]+D_\mathrm{KL}[q(x), p_w(x)] $$

と定義します．最右辺の第一項は真の分布のエントロピーで $\hspace{-0.2em}\hspace{0.2em}w\hspace{-0.2em}\hspace{0.2em}$ に依りません．第二項は真の分布 $\hspace{-0.2em}\hspace{0.2em}q(x)\hspace{-0.2em}\hspace{0.2em}$ と確率モデル $\hspace{-0.2em}\hspace{0.2em}p_w(x)\hspace{-0.2em}\hspace{0.2em}$ のKL divergenceになっています．つまり，真の分布に“近い”モデルほど， $\hspace{-0.2em}L(w)\hspace{-0.2em}\hspace{0.2em}$ の値が小さくなります．よって，真の分布に対して最適なパラメータの集合 $\hspace{-0.2em}\hspace{0.2em}W_0\hspace{-0.2em}\hspace{0.2em}$ を

$$ W_0\coloneqq\{w\in W; L(w)\text{が最小値をとる}\} $$

と定義してやることができます．ただし，異なる $\hspace{-0.2em}\hspace{0.2em}w_0, w_0'\in W_{0}\hspace{-0.2em}\hspace{0.2em}$ が同じ確率分布を表すとは限りません．同様に，真の分布を実現するパラメータの集合 $\hspace{-0.2em}\hspace{0.2em}W_{00}\hspace{-0.2em}\hspace{0.2em}$ を

$$ W_{00}\coloneqq\{w\in W; D_\mathrm{KL}[q(x), p_w(x)]=0\} $$

と定義できますが，空集合のこともあります．

経験対数損失関数 $\hspace{-0.2em}\hspace{0.2em}L_n(w)\hspace{-0.2em}\hspace{0.2em}$ を

$$ L_n(w)\coloneqq-\cfrac{1}{n}\sum_{i=1}^n\log{p(X_i|w)} $$

と定義し，サンプルの現れ方に対する平均値を取ると．

$$ \mathbb{E}[L_n(w)]=\int\prod_{i=1}^n(\mathrm{d}x_i)\,\left(-\cfrac{1}{n}\sum_{i=1}^n\log{p(x_i|w)}\right)\prod_{i=1}^nq(x_i)=-\int\mathrm{d}x\,q(x)\log{p_w(x)}=L(w) $$

より平均対数損失関数に一致します．

平均誤差関数と経験誤差関数

パラメータが $\hspace{-0.2em}\hspace{0.2em}w\in W, w_0\in W_0\hspace{-0.2em}\hspace{0.2em}$ の確率モデルについて，対数尤度比関数 $\hspace{-0.2em}\hspace{0.2em}f(x, w_0, w)\hspace{-0.2em}\hspace{0.2em}$ を

$$ f(x, w_0, w)\coloneqq \log{\cfrac{p_{w_0}(x)}{p_w(x)}} $$

と定めます．以降は真の分布を実現可能，つまりず $\hspace{-0.2em}\hspace{0.2em}W_{00}\hspace{-0.2em}\hspace{0.2em}$ は空集合でないと仮定します．このとき，$w_0\hspace{-0.2em}\hspace{0.2em}$ の選び方に依存せず $\hspace{-0.2em}\hspace{0.2em}p_{w_0}(x)=q(x)\hspace{-0.2em}\hspace{0.2em}$ なので，$f(x, w_0, w)\hspace{-0.2em}\hspace{0.2em}$ を単に $\hspace{-0.2em}\hspace{0.2em}f(x, w)\hspace{-0.2em}\hspace{0.2em}$ と書くことにしましょう．これを用いて平均誤差関数 $\hspace{-0.2em}\hspace{0.2em}K(w)\hspace{-0.2em}\hspace{0.2em}$ と経験誤差関数 $\hspace{-0.2em}\hspace{0.2em}K_n(w)\hspace{-0.2em}\hspace{0.2em}$ を

$$ K(w)\coloneqq\int\mathrm{d}x\,q(x)\,f(x, w)=\int\mathrm{d}x\,q(x)\log{\cfrac{q(x)}{p_w(x)}}=D_\mathrm{KL}[q(x), p_w(x)]\geq0 $$

$$ K_n(w)\coloneqq\cfrac{1}{n}\sum_{i=1}^nf(x, w)=\cfrac{1}{n}\sum_{i=1}^n\log{\cfrac{q(X_i)}{p_w(X_i)}} $$

と定めます．平均誤差関数を用いると，真の分布を実現するパラメータの集合は

$$ W_0=\{w\in W; K(w)=0\} $$

と書き直せます．

しりたいもの

知りたいものは，事後分布による平均操作

$$ \mathbb{E}_w[-]\coloneqq\cfrac{\displaystyle\int\mathrm{d}w\,(-) \exp(-nK_n(w))\varphi(w)}{\displaystyle\int\mathrm{d}w\, \exp(-nK_n(w))\varphi(w)} $$

が，サンプル数を増やすとどのように収束するかです．これは，事後微小積分

$$ \Omega(w)\mathrm{d}w\coloneqq\exp(-nK_n(w))\varphi(w)\mathrm{d}w $$

の $\hspace{-0.2em}\hspace{0.2em}n\to\infty\hspace{-0.2em}\hspace{0.2em}$ でのふるまいを調べることに帰着します。

$\hspace{0.2em}W_0\hspace{-0.2em}\hspace{0.2em}$ が一点からなるとき，適当な条件を課せば事後分布が正規分布で近似できることが知られています．それでは， $\hspace{-0.2em}W_0\hspace{-0.2em}\hspace{0.2em}$ が一般の集合の場合は $\hspace{-0.2em}\hspace{0.2em}n\to\infty\hspace{-0.2em}\hspace{0.2em}$ でどのようにふるまうのでしょうか．

特異点

既約な代数的集合 $\hspace{-0.2em}\hspace{0.2em}V\hspace{-0.2em}\hspace{0.2em}$ 上で $\hspace{-0.2em}\hspace{0.2em}0\hspace{-0.2em}\hspace{0.2em}$ となる多項式全体の集合を $\hspace{-0.2em}\hspace{0.2em}\mathbb{I}(V)\hspace{-0.2em}\hspace{0.2em}$ ，その生成元を $\hspace{-0.2em}\hspace{0.2em}f_1(x), f_2(x), \dots, f_r(x)\hspace{-0.2em}\hspace{0.2em}$ とします：

$$ \mathbb{I}(V)=\langle f_1, f_2, \dots, f_r\rangle $$

Jacobi行列

$$ J(x)\coloneqq　\left( \begin{array}{cccc} \cfrac{\partial f_1(x)}{\partial x_1} & \cfrac{\partial f_1(x)}{\partial x_2} & \ldots & \cfrac{\partial f_1(x)}{\partial x_d} \\ \cfrac{\partial f_2(x)}{\partial x_1} & \cfrac{\partial f_2(x)}{\partial x_2} & \ldots & \cfrac{\partial f_2(x)}{\partial x_d} \\ \vdots & \vdots & \ddots & \vdots \\ \cfrac{\partial f_d(x)}{\partial x_1} & \cfrac{\partial f_d(x)}{\partial x_2}& \ldots & \cfrac{\partial f_d(x)}{\partial x_d} \end{array} \right) $$

の階数の最大値を $\hspace{-0.2em}\hspace{0.2em}d_0\hspace{-0.2em}\hspace{0.2em}$ とおいたとき，点 $\hspace{-0.2em}\hspace{0.2em}x'\hspace{-0.2em}\hspace{0.2em}$ が特異点であるとは

$$ \mathrm{rank}(J(x')) < d_0\coloneqq \min_{x\in V}\mathrm{rank}(J(x)) $$

が満たされることを指します．

実は $\hspace{-0.2em}\hspace{0.2em}W_0\hspace{-0.2em}\hspace{0.2em}$ に特異点があるとき，そのままの形では特異点で $\hspace{-0.2em}\hspace{0.2em}n\to\infty\hspace{-0.2em}\hspace{0.2em}$ の極限をwell-definedには取れないことがわかります．

特異点解消をざっとみる

特異点解消定理

特異点解消定理はHironakaのフィールズ賞受賞業績として有名です．今回用いる特異点解消定理はAtiyahによるもので，特異点を“解消”はしないけれど，扱いやすい形に変えられるよという定理です．証明ですか？しりません．

開集合 $\hspace{-0.2em}\hspace{0.2em}W\subset\mathbb{R}^d\hspace{-0.2em}\hspace{0.2em}$ 上の解析関数 $\hspace{-0.2em}\hspace{0.2em}K\colon W\to\mathbb{R}\hspace{-0.2em}\hspace{0.2em}$ が非負で，零点を持つとする．このとき，ある $\hspace{-0.2em}\hspace{0.2em}d\hspace{-0.2em}\hspace{0.2em}$ 次元解析多様体 $\hspace{-0.2em}\hspace{0.2em}\mathcal{M}\hspace{-0.2em}\hspace{0.2em}$ と解析写像 $\hspace{-0.2em}\hspace{0.2em}g\colon\mathcal{M}\to W\hspace{-0.2em}\hspace{0.2em}$ が存在し， $\hspace{-0.2em}\mathcal{M}\hspace{-0.2em}\hspace{0.2em}$ の局所座標ごとに次の2式を満たす：

$$ K\circ g(u)=\prod_{i=1}^d {u_i}^{2k_i} $$

$$ |g'(u)|=b(u)\left|\prod_{i=1}^d {u_i}^{h_i}\right| $$

ただし， $\hspace{-0.2em}b(u)\hspace{-0.2em}\hspace{0.2em}$ は非負で解析的． $\hspace{-0.2em}\{k_1, k_2, \dots, k_d\}, \{h_1, h_2, \dots, h_d\}\hspace{-0.2em}\hspace{0.2em}$ は非負整数からなる集合(多重指数)で，それぞれ少なくとも1つの要素が非零．

おきもち

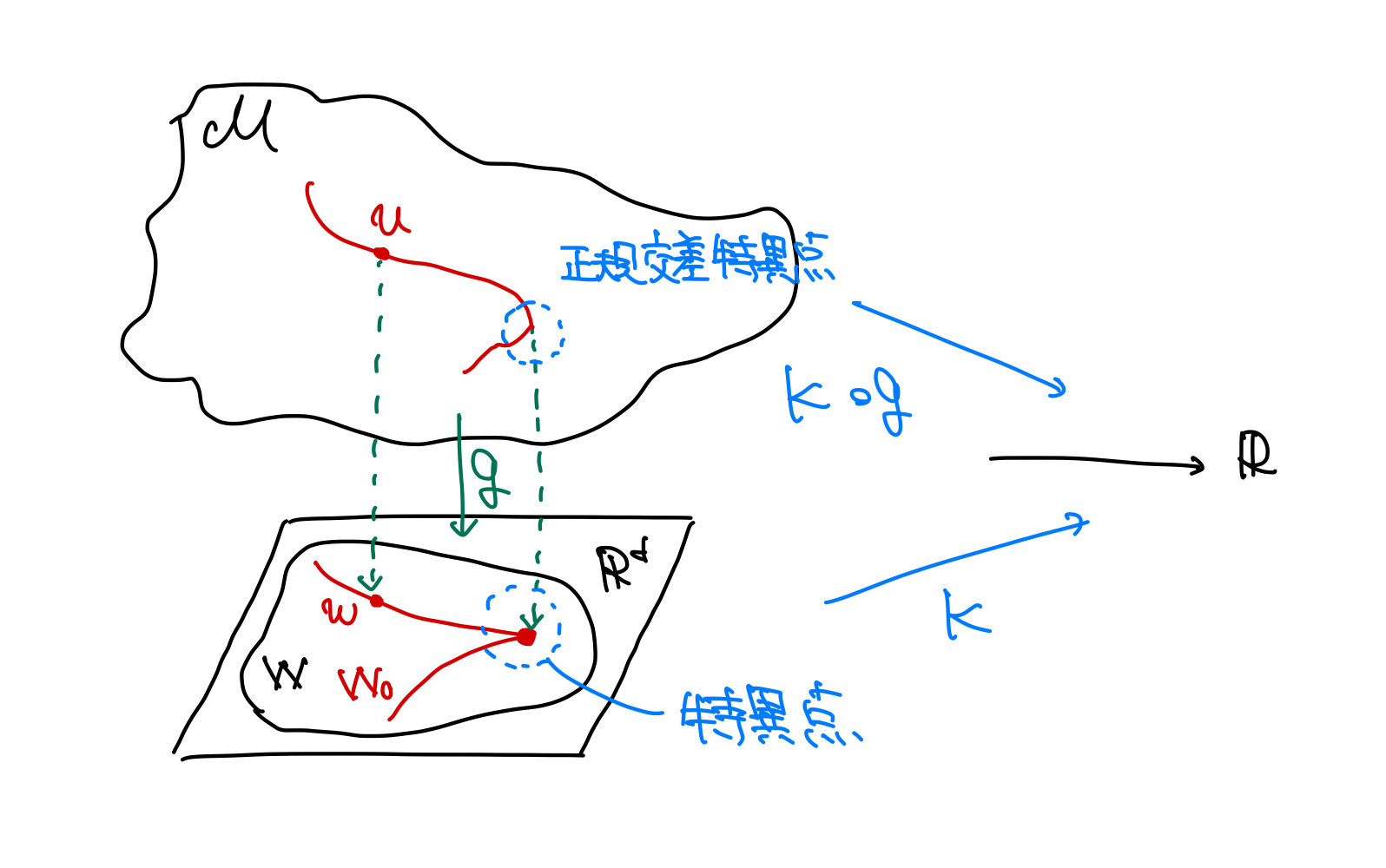
このように局所座標の積でかけるとき，関数 $\hspace{-0.2em}\hspace{0.2em}K\circ g\hspace{-0.2em}\hspace{0.2em}$ は点 $\hspace{-0.2em}\hspace{0.2em}u\hspace{-0.2em}\hspace{0.2em}$ で正規交差だといいます．この特異点解消定理は，たとえ関数 $\hspace{-0.2em}\hspace{0.2em}K\hspace{-0.2em}\hspace{0.2em}$ に特異点があったとしても，適当な多様体からの写像との合成を考えれば，正規交差なものに変換できることを示しています．解析関数が $\hspace{-0.2em}\hspace{0.2em}K_1, K_2\hspace{-0.2em}\hspace{0.2em}$ と2つある場合も，積 $\hspace{-0.2em}\hspace{0.2em}K_1K_2\hspace{-0.2em}\hspace{0.2em}$ を考えれば，これらの同時特異点解消も可能です。

特異点解消定理を適用する

平均誤差関数と事前分布の積 $\hspace{-0.2em}\hspace{0.2em}K(w)\cdot\varphi(w)\hspace{-0.2em}\hspace{0.2em}$ に特異点解消定理を適用すると，ある解析多様体 $\hspace{-0.2em}\hspace{0.2em}\mathcal{M},\hspace{-0.2em}\hspace{0.2em}$ 解析関数 $\hspace{-0.2em}\hspace{0.2em}g\colon \mathcal{M}\to W,\hspace{-0.2em}\hspace{0.2em}$ $\hspace{-0.2em}\hspace{0.2em}a\colon\mathbb{R}^N\times\mathcal{M}\to\mathbb{R},\hspace{-0.2em}\hspace{0.2em}$ $\hspace{-0.2em}\hspace{0.2em}b\colon\mathcal{M}\to\mathbb{R},\hspace{-0.2em}\hspace{0.2em}$ 多重指数 $\hspace{-0.2em}\hspace{0.2em}k, h\hspace{-0.2em}\hspace{0.2em}$ が存在し，

$\hspace{-0.2em}K\circ g(u)=u^{2k}\hspace{0.2em}$
$\hspace{-0.2em}f(x, g(u))=a(x, u)u^k\hspace{0.2em}$
$\hspace{-0.2em}\varphi\circ g(u)|g'(u)|=b(u)u^h\hspace{0.2em}$

がなりたつことが示せます．

経験過程を

$$ \xi_n(u)\coloneqq\cfrac{1}{\sqrt{n}}\sum_{i=1}^n\left(u^k-a(X_i, u)\right) $$

と定義すると，これは確率変数です．経験誤差関数について，経験過程を用いた標準形が得られます：

\begin{align*} nK_n(g(u))&=\sum_{i=1}^nf(X_i, g(u))\\ &=\sum_{i=1}^na(X_i, u)u^k\\ &=nu^{2k}-\sqrt{n}u^k\xi_n(u) \end{align*}

また，事後分布は

\begin{align*} \varphi(w)\mathrm{d}w&=\varphi(g(u))|g'(u)|\mathrm{d}u\\ &=b(u)|u^h|\mathrm{d}u \end{align*}

と表せます．以上より、事後微小積分の表記

\begin{align*} \Omega(w)\mathrm{d}w&=\exp(- nK_n(w))\varphi(w)\mathrm{d}w\\ &=\exp(-nu^{2k}+\sqrt{n}u^k\xi_n(u))|u^h|b(u)\mathrm{d}u \end{align*}

が得られました． $\hspace{-0.2em}n\to\infty\hspace{-0.2em}\hspace{0.2em}$ でも変化する $\hspace{-0.2em}\hspace{0.2em}\sqrt{n}u^k\hspace{-0.2em}\hspace{0.2em}$ の部分と，正規確率過程に法則収束するゆらぎ $\hspace{-0.2em}\hspace{0.2em}\xi_n(u)\hspace{-0.2em}\hspace{0.2em}$ の部分に分けられることがわかります．

参考文献

『代数幾何と学習理論』渡辺澄夫
『ベイズ統計の理論と方法』渡辺澄夫

Twitter	@PhysicsLab_2022
Mail	physlab2022[at]gmail.com