構造を持ちながら複雑な振舞いを見せるカオス、システム全体で模様を形成するパターン形成、リズミカルな振動が互いに歩調を合わせる同期現象に関する、身近な材料を使って出来る実験・観察および現象に対する数学的なモデルの解析を通して、これらのダイナミックで不思議な現象に普遍的に横たわる数学的構造に対する理解を深めることを目指します。（文・玉井 敬一）

非線形科学とは？

水面の模様。雲の流れ。生命の拍動。少し見渡すと、私たちが生きている自然界は活き活きとした動きに満ちており、それは時に、意外な現象として私たちの前に姿を現します。このダイナミックな自然の不可思議は、古来私たちを惹きつけてやみません。

このような自然の動きをいざ理解しようとするならば、自然の各要素について今までに得られた成果を踏まえながらも、自然のシステムを「独立した要素の集合体」と見なしてひとつひとつの要素を解析してゆく伝統的な発想を越え、システム全体として起きている「現象」のレベルに留まって普遍的な構造・メカニズムを探求する姿勢が必要です。これが「非線形科学」の目指すところであり、私ども「非線形科学班（非線形班）」が興味を持って取り組んでいることなのです。

非線形科学が扱う話題の範囲は極めて広いですが、非線形班では、異なる種類の粉体（後述）が円筒内でパターンを形成する「粉体の回転による軸性偏析」、原理は簡単でありながら複雑（カオス）な振舞いを示す事で知られている「揺れるアトウッドの機械」、身近な材料で簡単に作れて、意外かつ興味深い現象を示す「ペットボトル振動子」の3つを取り上げます。あとでそれぞれの記事で紹介します通り、これらの現象は実験の規模が日常生活レベルで比較的親しみやすいだけでなく、私たちの身近に見られる他の事柄と浅からぬ関わりを持っています。

会場では、それぞれのテーマについて過去の研究で分かっている事を紹介しつつ、私たちなりに調べてみたことを報告および実際に行った実験の一部を演示することによって、非線形科学の、普遍的な構造を探求する基礎科学としての可能性をお伝えしつつ、感じ取ったことをお互いに共有出来ればと考えています。短い間ではございますが、ご一緒に楽しんで頂けたら、そして多様で豊かな自然に思いを巡らせるきっかけになれば、この上ない幸いです。

それでは、私たちが一緒に探検する「非線形」の世界を、以下で少しだけ覗いてみることにしましょう。

粉体の回転による軸性偏析

タイトルからして、馴染みのない方にとって如何にも取っ付きづらそうではありますが、実際には、名前から受けるイメージほど複雑な実験を行っているわけではありません。

まず「粉体」という言葉を初めて聞く、という方も少なくないと思います。粉体とは、多くの細かい粒が集まったもののことを言い、ビーズや砂、ゴマなど私たちの身の回りにもたくさんあるものです。しかし、それだけ身近なものでありながら、いざ物理学の対象として粉体を扱おうとすると、1つ1つの粒の集まりとして扱うには粒子の数が多過ぎる上にそれぞれがどのように相互作用しているかが分かりづらく、そうかと言って単純に流れるもの（流体）のように扱っていては上手くいかない場合が少なからずあり、実はなかなか難しい（裏を返せば、面白い！）対象なのです。

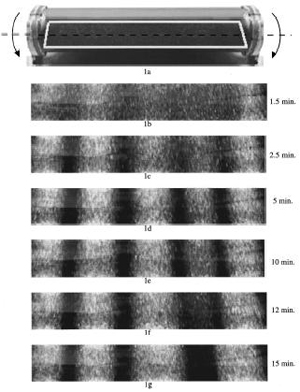セグリゲーション

そして、この難しさゆえに現状ではしばしば「経験とカン」で扱われる粉体の振舞いを体系的に理解することは、粉体を扱う機器の設計のように直接的な応用の可能性があるだけでなく、あるいは粉体を理解するときの考えが交通渋滞のような現象を理解するヒントになると考えられています。

さて、ここで扱うテーマである「回転による軸性偏析」ですが、これは、2種類の異なる材質・大きさの粉体を混合し、円筒に入れてしばらく回転させると、次第に2種類の粉体が回転軸に沿って分離（偏析）してゆくというものです。この現象自体は今から70年以上前の1939年に日本人の大山義年に発見されたのですが、未だ統一的な見方が完成しておらず、異なる種類の粉体を混ぜ合わせること（セメントやコンクリートをイメージすると良いかもしれません）が多い工学からの需要もあって、今日でも実験、コンピュータによるシミュレーション、数学的なモデルの解析、などなど様々なアプローチによって研究が進められています。

この五月祭では、粉体が分離する様子をシミュレーションと実際の装置を使った実験の両方でお見せしつつ、粉体の種類やパイプの回転数と分離の様子の関係を探求してゆきます。

揺れるアトウッドの機械

「カオス」という言葉をご存じでしょうか。英和辞典で “chaos” を調べると「大混乱」「無秩序」などと訳される通り、ごちゃごちゃと良く分からない状態になっている事を指す言葉として、数学や物理学に携わっていない人の間にもいくらか浸透した印象が有ります。

但し、少なくとも物理学や数学の用語としての「カオス」の意味の説明としては、「大混乱」「無秩序」というのは必ずしも当てはまりません。確かに、カオスな振舞いを示すシステム（以下「カオスなシステム」）に於いては、初期条件の僅かなズレが、時間とともにどんどん大きくなっていってしまい、たとえば運動を始めてちょうど1分後にどういう状態にあるかを正確に事前予測するというのは限りなく困難であり、その意味でカオスなシステムは「予測不可能」とは言えるでしょう。しかし、「予測不可能」は必ずしも「無秩序」を意味しません。それは単にシステムが規則に従って動いているというだけの話ではなく（システムが動く規則が分かっていても「予測不可能」であるからこそカオスは不思議なのです）、カオスなシステムが描く軌跡には、パイを引き延ばして折り畳む「パイこね」の操作を繰り返したような特徴的な構造が見られるのです。カオスにまつわる理論は気象学などに応用されているだけでなく、最近では、カオスに特徴的な構造を利用してカオスを制御したり、秘匿通信へ応用したりするための研究が行われています。

ここまでで「カオスなシステム」という言葉を使っていますが、では実際問題として、どのくらい複雑なシステムだと「カオス」になるのか、という疑問を持たれる方もいらっしゃるかもしれませんが、実は、一見してかなり単純そうなシステムでもカオスになり得るのです。

今回ご紹介する「揺れるアトウッドの機械」も、かなり単純でありながらカオスになるシステムの一例です。「アトウッドの機械」というのは、重さの違う2つのおもりを糸の両端につけて、滑車に通して手を離すと重い方のおもりが落ちてゆく（至極当然！）というもので、ニュートンの運動の法則を実験的に確かめるためにジョージ・アトウッドによって開発されました。その「アトウッドの機械」で、軽い方のおもりを左右に振らせるようにすると、初期条件によってカオスな振舞いを示すことが分かっています。そこで、この五月祭では、揺れるアトウッドの機械が、単純そうな見かけに反して複雑な振舞いを示す事を演示しつつ、観測データからカオスに特徴的な構造を見出すことを目標にして研究活動を行っています。

ペットボトル振動子

少しの道具があればキッチンでも出来る簡単な実験をご紹介しましょう。ペットボトルに水を入れ、キャップを開けっぱなしにしたままペットボトルをひっくり返すと水がどぼどぼと流れて落ちていくのは誰もが知っていることです。しかし、ドリルで穴を開け、その穴に長さ 10 cmほどの細いパイプを挿したキャップをして同じようにペットボトルをひっくり返すと、しばらくして水の流れが一旦止まり、「ぼこっ」と泡が昇って、再び水が流れまた泡が昇って…という周期的な運動になるのです。このような装置を、運動の様子をバネ（振動子）の振動運動に見立てて「ペットボトル振動子」と呼びます （Fig.）。

「何故こういう振動が起きるのか？」というのも不思議ですが、ペットボトル振動子について更に興味深いことがあります；複数のペットボトル振動子をビニールチューブ（ホース）で繋いでペットボトル振動子を「振動」させると、徐々に振動の様子が揃ってくる「同相同期」や泡の上昇が交互に起こる「逆相同期」をはじめとして様々な同期現象が起きるのです。しかも、同期の性質（同相・逆相など）は、ペットボトル振動子を繋ぐホースに水を入れたか入れないかでおおよそ制御できるのです。

実は同期現象というものはペットボトル振動子に限って起きるものではありません。寧ろ、同期現象と関連すると考えられるものは多岐にわたって確認されています：超伝導や心筋細胞、はたまたコンサート会場での拍手まで（脚注：但し、拍手の同期には文化差があります）！そのように身の回りの様々なところに同期が見られるからこそ、ペットボトル振動子のような、簡単に作れてなおかつ解析も比較的簡単な場合に関して考察することが、同期現象に普遍的に潜む構造をあぶり出すためのヒントになるのではないかと考えられるのです。

そこで、この五月祭では、既に報告されている2つのペットボトル振動子の同期現象を紹介しつつ、3つ以上が結合した場合にも関心の対象を拡げ、より多くの数のペットボトル振動子が結合した場合に、ホースに水を入れるか否かが同期の性質をどのように決定するかを予想し、実験的に確認する・理論的に裏付けすることを目指しています。

興味がある方へのコラム: 現象の特徴を捉えるには？

よく知られた人物の似顔絵を描くことを想像してみて下さい。人の顔は案外複雑で、正確に再現しようとすれば、あまりに膨大な量の情報が必要ですが、完璧な再現を目指さずとも、その人の特徴を捉えていれば、少なくとも描かれている人物が誰かを伝えることは出来ます。

似たような要領で、一部の情報を切り捨てて現象の特徴を抽出するということを考えることができます。全ての場合に通用する万能の方法は知られていませんが、ここでは振動子の同期を例にそのアイデアをごく簡単かつ大雑把に紹介しておきます。

一定の周期を持った振動には、振動の1周期の中でどの状態にあるかを表す「位相」という量が定義できます。いま、一定の周期をもって振動するものを振動子と呼び、性質が似た2つの振動子が結合している場合を考えると、それぞれの振動子はお互いの相互作用によってかく乱を受けている格好になります。そこで、（詳細はここでは省略しますが）撹乱を受ける前に定義した位相を、かく乱を受けた状態にまで拡張することで、振動子の運動を記述するもとの式を、位相に関する式に焼き直してやります。そうすると、両方の振動子の位相差を考えることができるようになり、2つの振動子が同期するか、するとしてどのような同期に至るかを捉えやすくなるのです。

上で振動子についての情報から位相についての情報を抽出して、同期現象に対する見通しを良くしたように、システムを記述するもとの式を、興味がある現象の特徴を損なわない範囲で簡単化する方法は「縮約」と呼ばれ、そのままでは理論的に扱いにくいシステムを扱うことが多い非線形科学で不可欠な理論的手段になっています。

参考文献

• 『非線形科学』（蔵本由紀、集英社新書）
  一般の方向け。非線形科学の各トピックをこの分野の研究者が紹介しています。
• 『非線形・非平衡の数理』シリーズ（三村昌泰監修、東京大学出版会）
  微分方程式を扱える大学生以上向け。トピックを紹介しつつ、「縮約」の方法などの技術的な部分の解説もなされています。

主な活動メンバー

非線形班では、3つの実験テーマに対応する小さなグループに分かれて活動しています。それぞれのグループについて、物理学科の4年生が3名前後、3年生が1-2名所属して精力的に研究活動に当たっています。