情報熱力学班の紹介

Research topic 1 ~マクスウェルの悪魔と情報熱力学~

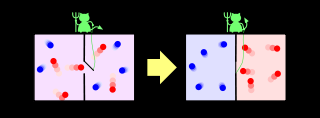
箱がしきりで2つに仕切られていて、しきりには小さな穴が開いています（ここから気体分子が出入りできます）。2つの部屋には同じ温度の気体が入っていて、何もしなければずっとこの温度のままです。しかし仕切りの穴の部分に「悪魔」がいて、穴を通ろうとする分子の速さを見て、速い分子だけを右側に通すとします。この時右側の箱は左側よりも速い分子が多くなり、2つの箱に温度差ができたことになります。

エントロピー増大は確率的なもの、あるいは平均的に成り立つものだといいました。しかし平均をとらず、一回の熱のランダム過程においては、エントロピーを減らす、あるいは熱が仕事になるような事象がたまに起こりえます（上の例では、速い分子がとおろうとすること）。これを「観測」して、それに応じ「フィードバック（速い分子のみを通すこと）」すれば、エントロピーを下げることができるのです！

このように、観測とフィードバックという「情報」を使えば、熱を仕事に変えることができるということが最近になってわかり始め、さらに2010年には一般化された熱力学第二法則が、当時東大の上田教授の院生であった沙川准教授によって示されました。さらに、この沙川上田等式は、東大の佐野教授、中央大の鳥谷部助教（当時）、中央大の宗行教授によって実験的にも検証されました。これらの理論体系は「情報熱力学」として定式化され、現在も盛んに研究されています。同時に、観測により「悪魔」が持つ「記憶」のエントロピーが増え、この記憶も含めた全体のエントロピーを考えると第二法則には反さず、パラドックスではないことも定量的に理解されました。

今回の展示では、粉体（ガラスビーズ）を加振することで、熱力学に擬似した状況を作り、沙川上田等式は成り立つのか、変更を受けるのかについて検証します。さらに、「マクスウェルの悪魔」を体験するシミュレーションゲームを作り、熱力学第二法則がどのようなものかを体験してもらいたいと思います。

Research topic 2 ~ブラウンラチェットとパロンドのパラドックス~

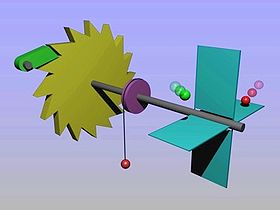
棒の一端には羽根車があり、もう一端には非対称な歯車があるとしましょう。歯車には爪があり、一方向のみの運動を許す整流作用があるとします。これを等温の気体に入れると、羽根車に分子がランダムに当たった時、棒でつながれた歯車もプルプル動きます。この時たまに爪が持ち上げられ、歯車が回転するでしょう。こうして一方向のみに全体が回り、熱から力学的な運動を取り出す永久機関が作れそうです。これがブラウンラチェットの一例です。

実は、上の状況では、爪も熱的に揺らいでいるために、整流作用は失われ、歯車は回らないことが知られています。しかし、たとえば歯車の温度が羽根車より低ければ一方行に回ることも知られています（ただしこの場合、放っておくと二つの温度が等しくなるので、永久機関にはなりません）。このように、非対称ポテンシャルを利用して熱揺らぎを一方向の運動に変える一連のモデルが、ブラウンラチェットとして研究されてきています。これらを研究することで、たとえば生体内の分子モーターなどが理解できると期待されています。

これらのモデルは、熱的な物以外とも関連しています。その一つがパロンドのパラドックスと呼ばれるゲームです。2つの「負け続ける」コイン投げのゲームをランダムに行うと「勝ち続ける」ようになるという不思議な話なのですが、ブラウンラチェットとの関連とともに研究されています。

今回の展示では、ランダムな動きや周期的な動きから、どのようにして一方向の運動が取り出せるのか解説いたします。また、パロンドのパラドックスのシミュレーションなども行います。

展示内容

粉体を用いた確率分布、非平衡、マクスウェルデーモンの説明

粉体（ガラスビーズ）を加振すると、ランダムに動く状況が作られます。粒子（粉体）が熱浴（加振器）に接しているとみなして、熱力学の種々の言葉の意味を感覚的につかんでいただきたいと考えています。

「情報熱力学」のポスター展示

近年発展した分野である情報熱力学を、日常の例から初めて、わかりやすくポスターで解説いたします。一般向けのポスターと発展のポスターに分けて展示する予定です。

粉体系における沙川上田等式の検証（ポスター）

粉体を用いてフィードバックコントロールの実験を行い、（擬似的な意味で）従来の熱力学第２法則をやぶるという実験を行いました。

また、上に述べた粉体系と熱系のアナロジーは、実際には正しくはありません。粉体系を熱系とみなして沙川上田等式を適用し、成り立っているかということも検証しました。

当日は、これらの実験方法と結果について研究成果を発表いたします。

「ラチェット」のポスター展示

研究topicでも述べたように、非対称なポテンシャルを用いて一方向の運動をとりだすラチェット機構が知られています。これについて解説いたします。

シミュレーション

特にマクスウェルデーモンのゲーム、パロンドのパラドックスなど、実験展示でお伝えしきれなかった部分をシミュレーションという形で展示いたします。

謝辞

今回の班の企画を通じて、東京大学大学院理学系研究科物理学専攻　佐野雅己教授および佐野研究室の院生の方々、東京大学大学院総合文化研究所広域科学専攻相関基礎科学系　沙川貴大准教授および院生の方々に、機材、実験内容、理論など様々な面でサポートをいただきました。また、東京大学理学部物理学科　技術室の大塚さんには、機材の作成の面でお世話になりました。この場をお借りして、皆様に深く感謝申し上げます。

メンバー

4年

濱崎立資（班長）

秋津一之

足立大樹

飯田耀

周健司

高木隆司

龍田真美子

長谷川雅大

宮藤大輔

吉岡信行

吉田貴寿

3年

庄司泰萌

山浦豪将

参考記事

「Maxwellのデーモンと情報熱力学」沙川貴大、上田正仁著

http://cat.phys.s.u-tokyo.ac.jp/publication/Suri_Kagaku_Final_Version.pdf

・「情報熱力学の構築: ランダウアー原理を超えて」沙川貴大、上田正仁著

http://www.kurims.kyoto-u.ac.jp/~kyodo/kokyuroku/contents/pdf/1705-11.pdf

・「情報処理過程における熱力学第二法則」沙川貴大著

http://www.ieice.org/~netsci/wp-content/uploads/2012/01/NetSci201201_Sagawa.pdf

・「Maxwellの悪魔の実現」宗行英朗著

http://www.phys.chuo-u.ac.jp/j/muneyuki/?%5BMaxwell%27s+Demon%5D

参考文献

• ・関本謙「ゆらぎのエネルギー論」岩波書店（2004）
• ・U Seifert ”Stochastic thermodynamics, fluctuation theorems and molecular machines.” Reports on Progress in Physics(2012)
• ・S Toyabe, T Sagawa, M Ueda, E Muneyuki, M Sano “Experimental demonstration of information-to-energy conversion and validation of the generalized Jarzynski equality.” Nature Physics(2010)
• ・T Sagawa “Thermodynamics of information processing in small systems.” Progress of Theoretical Physics(2012)
• ・T Sagawa, M Ueda “Information Thermodynamics:Maxwell’s Demon in Nonequilibrium Dynamics.” arxiv(2011)
• ・GP Harmer, D Abbott, PG Taylor , JM Parrondo “Brownian ratchets and Parrondo's games.” An Interdisciplinary Journal of Nonlinear Science(2001)