はじめに

ごきげんよう．いぇとです． この記事は東京大学理学部物理学科 B3 有志による Physics Lab. 2022 Advent Calendar 2021 19日目の記事です．

Physics Lab. とは物理学科有志による五月祭企画です．私は生物物理班に所属しています．生物物理班については，たがやし班長が書いてくれた記事『生物物理班だよ』を見てください．絶対．

当初の予定では，19日目は統計力学のくりこみ群の話を書こうと思っていたのですが，多忙につき色々と試行錯誤をする暇がなく辞めることにしました．書いてもいいんですけどね．

代わりに LaTeX のお役立ち（？）情報を書こうと思います．この記事では LaTeX の基本事項を前提とします．今回は私が普段使っているパッケージの紹介や気をつけていることなどについてまとめます．（「普段気を付けていること」とかいうの，普段気を付けているせいで常に意識しているわけではなくてパッとは思いつかないです．この記事は私の過去のレポートや発表資料を見返しながら作成しています．）

（この記事では脚注をできるだけ付けずにカッコなどを使います．）

パッケージ

TikZ パッケージ

描画パッケージです．12日目の記事は TikZ について書きました．まだ読んでいない人はどうぞ：『TikZ でこけし・・Barnsley fern・トポロジカル欠陥』

physics パッケージ

とりあえずの physics パッケージです．いろんなコマンドが簡潔に書けます．プリアンブルでパッケージを読み込みます．

\usepackage{physics}

普段使っているコマンドをピックアップします．まずはカッコ関連．

• \qty(), \qty{}, \qty[]：カッコのサイズを勝手に調節してくれます．（\qty の綴りは quantity からきています．英語では \(\hspace{-0.2em}\hspace{0.2em}(x+1)(x+2)\hspace{-0.2em}\hspace{0.2em}\) を the quantity x plus one times the quantity x plus two と読むらしいです．）

\[
%\quad：スペースを空ける
\qty(\frac{3}{4})^n,\quad
\qty{\qty(\frac{3}{4})^n+\qty(\frac{4}{5})^n},\quad
\qty[\qty{\qty(\frac{3}{4})^n+\qty(\frac{4}{5})^n}+2^n]
\]

出力：

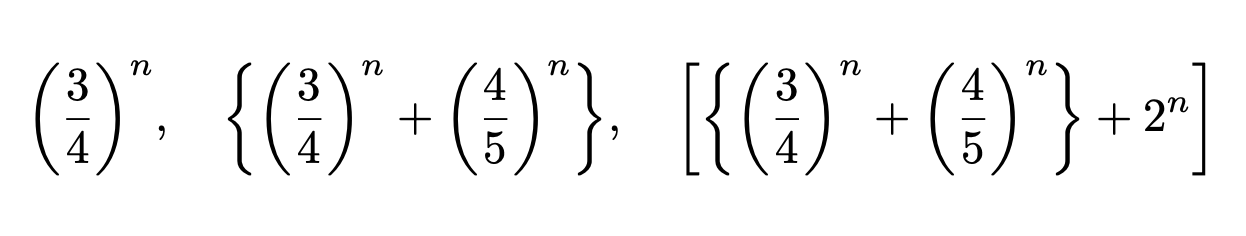
次に微分・偏微分・変分．

• \dd{}, \dd[]{}：微小量の \(\hspace{-0.2em}\hspace{0.2em}\mathrm{d}\)．\dd{x} で \(\hspace{-0.2em}\hspace{0.2em}\mathrm{d}x\hspace{-0.2em}\hspace{0.2em}\) を出力して，前後に適切なスペースを入れてくれます．\dd[3]{x} のようにすると \(\hspace{-0.2em}\hspace{0.2em}\mathrm{d}^3x\hspace{-0.2em}\hspace{0.2em}\) としてくれます．
• \dv{}：微分演算 \(\hspace{-0.2em}\hspace{0.2em}\mathrm{d}/\mathrm{d}x\hspace{-0.2em}\hspace{0.2em}\) を出力します．
• \dv{}{}：\dv{f}{x} のように入力を2つ入れると \(\hspace{-0.2em}\hspace{0.2em}\mathrm{d}f/\mathrm{d}x\hspace{-0.2em}\hspace{0.2em}\) を出力してくれます．
• \dv[]{}{}：\dv[n]{f}{x} のようにもう一つ引数を指定すると \(\hspace{-0.2em}\hspace{0.2em}\mathrm{d}^nf/\mathrm{d}x^n\hspace{-0.2em}\hspace{0.2em}\) としてくれます．
• \dv*{}{}：* をつけると微分をインライン表示してくれます．
• \pdv{}, \pdv{}{}, \pdv[]{}{}, \pdv*{}{} など：偏微分のコマンドです．挙動は \dv と同じ．
• \var{}, \fdv{} など：変分のコマンドです．挙動は \dd や \dv と同じ．

\[
\int f(x)\dd{x},\quad
\dv{f}{x},\quad
\pdv{f}{x},\quad
\fdv{f}{x}
\]

出力：

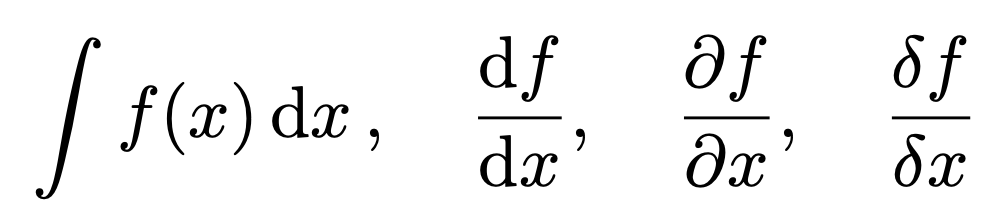
行列関連．

• \mqty(), \mqty[] など：行列が書けます．列は & で，行は \\ で区切ります．
• \dmat{}, \dmat[]{}：対角行列を出してくれます．\dmat[0]{} のように 0 を渡せば，ゼロで埋めてくれます．

\[
\mqty[0&1\\2&0],\quad
\mqty[\dmat{1,-1}],\quad
\mqty[\dmat[0]{1,-1}]
\]

出力：

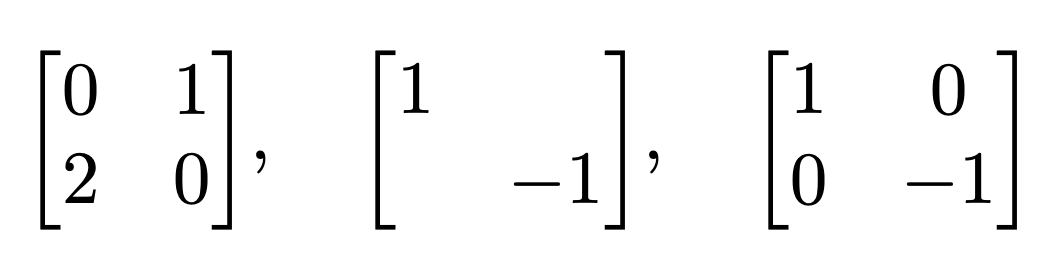
ブラケット記法．

• \bra{], \ket{}：ブラケットが書けます．
• \braket{}{}, \braket{}：内積が書けます．
• \ketbra{}{}, \ketbra{}：外積が書けます．
• \ev{}, \ev{}{}：期待値が書けます．
• \mel{}{}{}：行列要素が書けます．

\[
\bra{a},\quad
\ket{a},\quad
\braket{a}{b},\quad
\ketbra{a}{b},\quad
\ev*{\hat{A}}=\ev{\hat{A}}{n},\quad %resizeしたくないので*をつける
\mel{n}{\hat{A}}{m}
\]

出力：

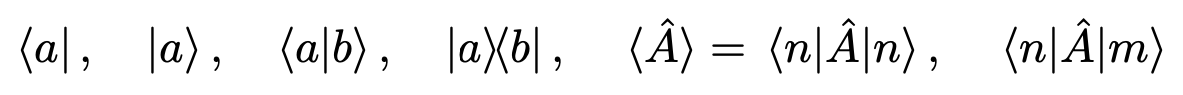
その他よく使うもの．

• \eval：評価（代入）．
• \order：オーダー．
• \cross：外積．
• \Re, \Im：実部と虚部．（もともと \Re で表示されていたものは \real に，\Im で表示されていたものは \imaginary に書き換えられています．）
• \qcc, \qif など：前後に \quad が入ります．ごく稀に使う．

\[
\int_1^\inf\frac{1}{x^2}\dd{x}
=\eval{-\frac{1}{x}}_1^\inf
=1.
%プリアンブルで \renewcommand{\inf}{\infty}
\]

\[
e^x
=1+x+\order{x^2}.
\]

\[
%プリアンブルで \usepackage{bm}
\bm{A}\cross\bm{B},\quad
z=\Re z+i\Im z
\]

出力：

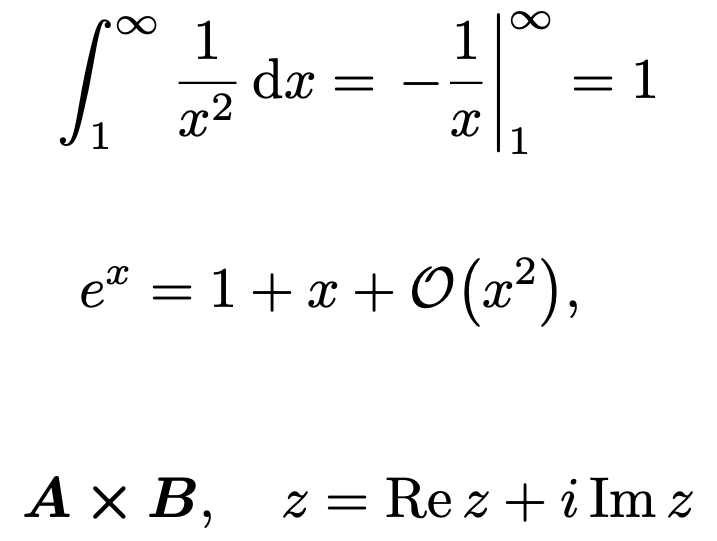
siunitx パッケージ

siunitx は SI 単位を出力するパッケージです．意外と知られていないみたいなのですが，物理学科生は知っておくべきパッケージの一つだと思います．パッケージの読み込みをプリアンブルでしておきます．

\usepackage{siunitx}

前提として，単位は必ず立体で書きましょう．たとえば \(\hspace{-0.2em}\hspace{0.2em}m/s\hspace{-0.2em}\hspace{0.2em}\) などと書かず \(\hspace{-0.2em}\hspace{0.2em}\mathrm{m}/\mathrm{s}\hspace{-0.2em}\hspace{0.2em}\) と書くべきだということです．siunitx パッケージはもちろんその点をカバーしてくれます．

siunitx には主に2種類のコマンド \si{}, \SI{}{} があります．

• \si{}：単位のみを表示する．\si{kg.m.s^{-2}} のようにすると \(\hspace{-0.2em}\hspace{0.2em}\mathrm{kg}\,\mathrm{m}\,\mathrm{s}^{-2}\hspace{-0.2em}\hspace{0.2em}\) を表示してくれます．
• \SI{}{}：数字も合わせて表示したい場合に使います．\SI{1.23e-3}{m} のようにすると \(\hspace{-0.2em}\hspace{0.2em}1.23\times10^{-3}\,\mathrm{m}\hspace{-0.2em}\hspace{0.2em}\) を表示してくれます．

いま例示したように，数字部分の表示もいろいろと対応してくれています．また，他にもいくつか便利なコマンドがあります．普段使っているものを紹介しておきます．多くは \si{} 内のみで有効なコマンドであることに注意してください．

• \ang{}, \degree：角度表示．\degree で \(\hspace{-0.2em}\hspace{0.2em}^\circ\hspace{-0.2em}\hspace{0.2em}\) 単体を表示します．\ang{15} で \(\hspace{-0.2em}\hspace{0.2em}15^\circ\hspace{-0.2em}\hspace{0.2em}\) を表示してくれます．
• \degreeCelsius：摂氏温度の単位 \(\hspace{-0.2em}\hspace{0.2em}^\circ\mathrm{C}\hspace{-0.2em}\hspace{0.2em}\) を表示します．
• \ohm：\(\Omega\hspace{-0.2em}\hspace{0.2em}\) を表示します．
• \micro：μ を表示してくれます．\(\mu\hspace{-0.2em}\hspace{0.2em}\) としないようにしましょう．

他にもできることはたくさんあるので，気になる人はパッケージのマニュアルを読んでください．

cancel パッケージ

cancel パッケージは数式で消えた項を明記する際に使います．いつも通りパッケージを読み込みます．そのままだと線が細くて不満が残るので，オプション thicklines をつけて線を太くしています．

\usepackage[thicklines]{cancel}

また，線を赤くしておきたいので，color パッケージを読み込んでおいて cancel パッケージの線の色を指定している \CancelColor を再定義しておきます．

\usepackage[thicklines]{cancel}
\usepackage{color}
\renewcommand{\CancelColor}{\color[rgb]{0.7,0,0}}
%少し暗めの赤

cancel パッケージで主に使うコマンドは \cancel, \bcancel, \xcancel の3つです． \cancelto というのもありますが，私はあまり使いません．

\begin{align*}
e^x-e^{-x}
&=\qty(\cancel{1}+x
		+\bcancel{\frac{x^2}{2}}+\frac{x^3}{3!}
		+\xcancel{\frac{x^4}{4!}}+\cdots)
	-\qty(\cancel{1}-x
			+\bcancel{\frac{x^2}{2}}-\frac{x^3}{3!}
			+\xcancel{\frac{x^4}{4!}}+\cdots)\\
&=2\qty(x+\frac{x^3}{3!}+\cdots)\\
&=2i\sin x.
\end{align*}

出力：

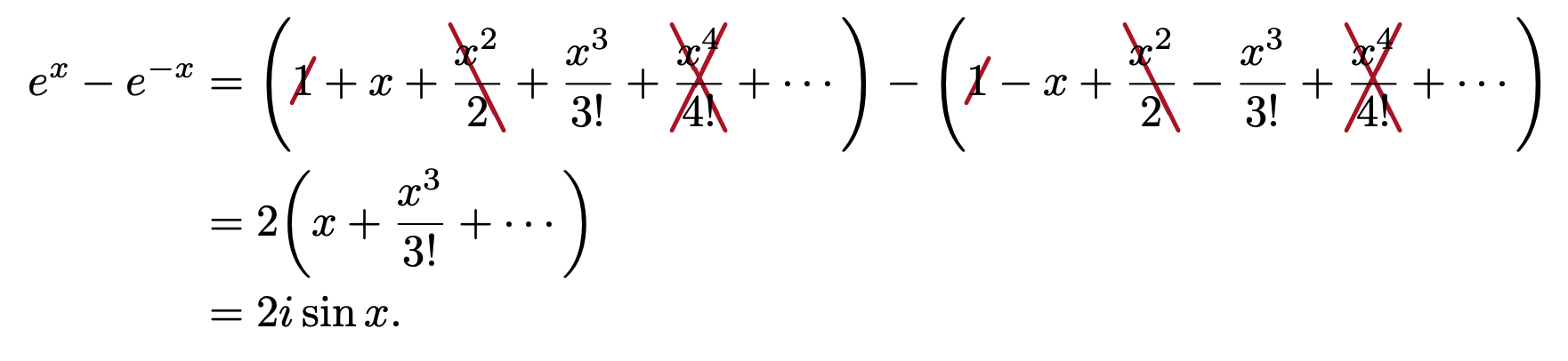
comment パッケージ

comment パッケージは文字通りコメントアウトのパッケージです．comment 環境で囲めば良いだけです．

数学や物理の
\begin{comment}
天才でなくても学科で学べば貢献できます．
もちろん
\end{comment}
天才は存分に活躍できます．

出力：

mhchem パッケージ

mhchem パッケージは化学式を書くためのパッケージです．\ce{} というコマンドを使います．たとえば \ce{H2O}, \ce{H+} などと使います．化学反応式も書けます．

\[
\ce{Ba(OH)2 + H2SO4 -> BaSo4 v + 2H2O}
\]

出力：

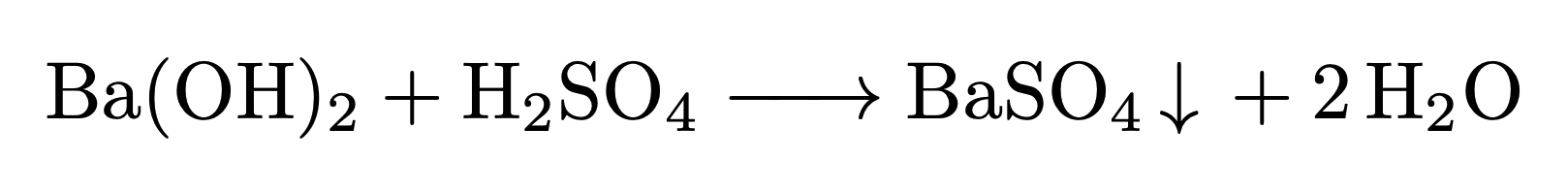
疲れたのでパッケージ紹介はこの辺にします．

数式環境

amsmath パッケージには多くの数式環境が備わっています．その中でも特に普段使いしているものを紹介します．

インライン数式とディスプレイ数式

ご存知の通りインラインの数式は $…$ で表示します．ディスプレイ数式は \[…\] を使います． （$$…$$ は推奨されていません．）

equation 環境・align 環境

単一行の数式で式番号を振る場合には equation 環境を用います．複数行の数式には align を多く使います．

\begin{equation}
…
\end{equation}

\begin{align}
…
\end{align}

式番号の参照

式番号の参照には \label{} と \ref{} または \eqref{} を用いるようにしましょう．式(1)のように手打ちをするとあとから修正を入れる際にかなり面倒です．図や表の番号の参照についても同様に \label{}, \ref{} を用いましょう．

Campbell-Baker-Hausdorff の公式は，演算子 $\hat{A},\hat{B}$ を用いて次のように書ける：
\begin{equation}
e^{\hat{A}}\hat{B}e^{-\hat{A}}
=\hat{B}+[\hat{A},\hat{B}]+\frac{1}{2}[\hat{A},[\hat{A},\hat{B}]]+\cdots.
\label{eq1}
\end{equation}

式\eqref{eq1}を用いて，演算子 $\hat{V}$ の相互作用表示は次のように書くことができる．

出力

式番号をつけるか否かについて少しコメントしておくと，私はほとんどの式に式番号を振るようにしています．ゼミや演習の発表などで使う際に式番号が振られていると話がしやすいからです．ただし，その式単体がメモ書き程度のあまり重要でないものであれば式番号を降らないこともあります．

また，参照した式番号だけに式番号をつけるという人もいるようです．そのようにしたい場合は mathtools パッケージを読み込んだ上で \mathtoolsset{showonlyrefs=true} とします．

gather 環境

gather 環境は，複数行の数式をすべて中央揃えで表示する環境です． align 環境などと同様に，gather* とすれば式番号を非表示にできます．

\begin{gather}
\nabla\cdot\bm{D}
=\rho\\
\nabla\cdot\bm{B}
=0\\
\nabla\cross\bm{E}
=-\pdv{\bm{B}}{t}\\
\nabla\cross\bm{H}
=\bm{j}+\pdv{\bm{D}}{t}
\end{gather}

出力：

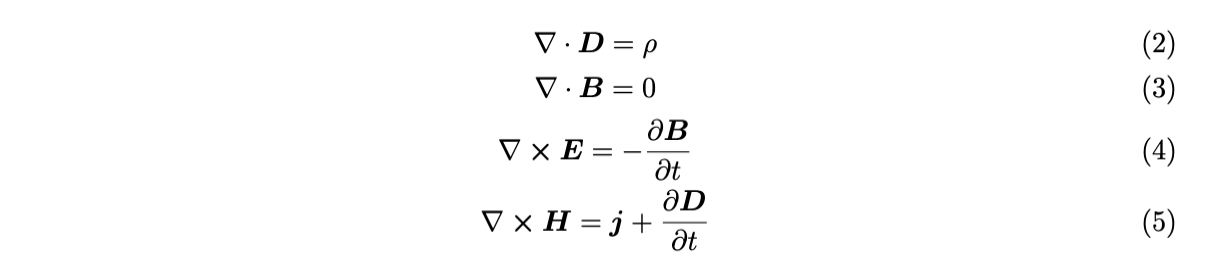
aligned 環境

aligned 環境は，他の数式環境（たとえば equation）の内部で用いる環境です．equation の内部で align 環境のようにできます．

\[
\begin{aligned}
\nabla\cdot\bm{D}
&=\rho\\
\nabla\cdot\bm{B}
&=0\\
\nabla\cross\bm{E}
&=-\pdv{\bm{B}}{t}\\
\nabla\cross\bm{H}
&=\bm{j}+\pdv{\bm{D}}{t}
\end{aligned}
\]

出力：

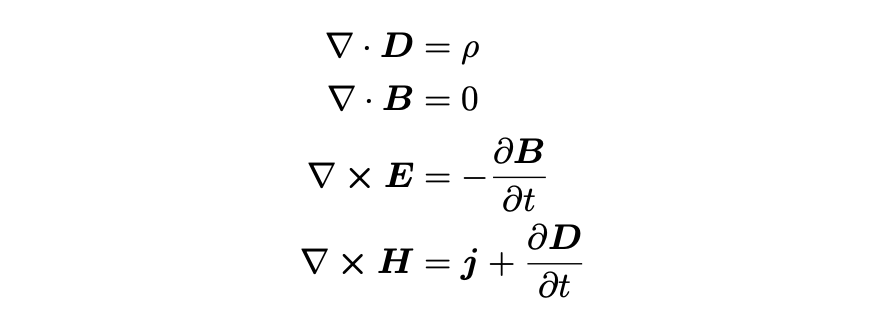
cases 環境

cases 環境は場合分けのような書き方ができます．挙動は aligned 環境と似ています．

\[
V(x)=
\begin{cases}
0		&(-a\le x\le a),\\
\infty	&(x<-a, x>a).
\end{cases}
\]

出力：

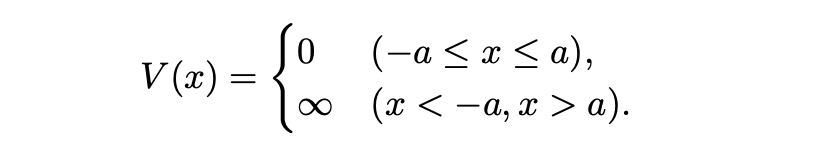
multlined 環境

multiluned 環境は，長すぎる式を複数行に折り返す際に用います．オプションで b,t を指定すると，どの位置を基準にするかを指定できます．

\[
\nabla^2f=
\begin{multlined}[t] %[t]で上の行を基準にする
\frac{1}{r^2}\pdv{r}(r^2\pdv{f}{r})
+\frac{1}{r^2\sin\theta}\pdv{\theta}(\sin\theta\pdv{f}{\theta})\\
+\frac{1}{r^2\sin^2\theta}\pdv[2]{f}{\phi}
\end{multlined}
\]

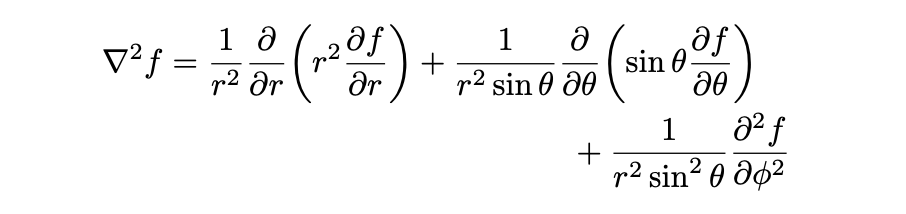
amsmath パッケージには他にも便利な数式環境があります．『amsmathの数式環境まとめ』がよくまとめられていると思うので，参照してください．

普段気を付けていること

文字列を立体で書く

何かの略であったり文字列そのものであったりという場合には，添字を立体にすべきだと思っています．たとえば \(\hspace{-0.2em}\hspace{0.2em}E_{in}\hspace{-0.2em}\hspace{0.2em}\) ではなく \(\hspace{-0.2em}\hspace{0.2em}E_\text{in}\hspace{-0.2em}\hspace{0.2em}\) とすべきだということです．

\text{} や \mathrm{} を用いると立体にできます．文字列という意味で私は \text{} を用いています．

相転移温度や Boltzmann 定数を書く場合にも，私は \(\hspace{-0.2em}\hspace{0.2em}T_\text{c}, k_\text{B}\hspace{-0.2em}\hspace{0.2em}\) と書くようにしています．こちらは1文字なので斜体のままでも良いとは思います．

添字ではないですが，\(\text{const}.\hspace{-0.2em}\hspace{0.2em}\) や \(\hspace{-0.2em}\hspace{0.2em}\text{odd}, \text{even}\hspace{-0.2em}\hspace{0.2em}\) なども立体で書くようにしています．

\(\hspace{-0.2em}\hspace{0.2em}\mathrm{d}\hspace{0.2em}\)

微小量を表す \(\hspace{-0.2em}\hspace{0.2em}\mathrm{d}\hspace{-0.2em}\hspace{0.2em}\) は立体で書くようにしています．\(\mathrm{d}x\hspace{-0.2em}\hspace{0.2em}\) のように，\(\mathrm{d}\hspace{-0.2em}\hspace{0.2em}\) は単体で意味をなさず複合体として何かの微小量を表すからです．これは私の好みの問題であって，必ずしも立体にすべきというわけではないと思います．（むしろ斜体にすべきだという人もいます．）

先ほど紹介したように physics パッケージに \dd{} というコマンドがあるのでそれを用いましょう．前後に適切なスペースを入れてくれます．

\(\hspace{-0.2em}\hspace{0.2em}\varDelta\hspace{0.2em}\)

\(\hspace{0.2em}\varDelta x\hspace{-0.2em}\hspace{0.2em}\) のように，\(x\hspace{-0.2em}\hspace{0.2em}\) の微小量という意味を持つ場合には \varDelta を用いています．一方で，\Delta すなわち \(\hspace{-0.2em}\hspace{0.2em}\Delta\hspace{-0.2em}\hspace{0.2em}\) は，それ単体で微小量を表す場合に用います．\(x+\Delta\hspace{-0.2em}\hspace{0.2em}\) のような使い方をするということです．

インラインの分数など

インラインで分数を書く場合があると思います．その際に \(\hspace{-0.2em}\hspace{0.2em}\frac{x}{y}\hspace{-0.2em}\hspace{0.2em}\) でも \(\hspace{-0.2em}\hspace{0.2em}\dfrac{x}{y}\hspace{-0.2em}\hspace{0.2em}\) でもなく \(\hspace{-0.2em}\hspace{0.2em}x/y\hspace{-0.2em}\hspace{0.2em}\) を用いるようにしています．\(\frac{x}{y}\hspace{-0.2em}\hspace{0.2em}\) は文字が小さすぎる，\(\dfrac{x}{y}\hspace{-0.2em}\hspace{0.2em}\) は行間が崩れるといった理由です．\(\dfrac{x}{y}\hspace{-0.2em}\hspace{0.2em}\) の方が可読性が高いのでこちらを使う人も多いと思います．行列の成分や指数，分母や分子に分数を書く際などで同じように \(\hspace{-0.2em}\hspace{0.2em}x/y\hspace{-0.2em}\hspace{0.2em}\) と書くようにしています．

新しい演算の定義

「気を付けていること」ではないと思いますが，新しい演算を定義する際には \DeclareMathOperator を使いましょう．スペースの調節などを自動で行ってくれます．たとえば \(\hspace{-0.2em}\hspace{0.2em}\mathrm{Log}\hspace{-0.2em}\hspace{0.2em}\) を定義したいときには次のようにしておけば良いです．

\DeclareMathOperator{\Log}{Log}

まれに，\(\sin x\hspace{-0.2em}\hspace{0.2em}\) を \(\hspace{-0.2em}\hspace{0.2em}sinx\hspace{-0.2em}\hspace{0.2em}\) と書く人がいます．\sin を使いましょう．

指数

\(\hspace{0.2em}x_0\hspace{-0.2em}\hspace{0.2em}\) の2乗を \(\hspace{-0.2em}\hspace{0.2em}x_0^2\hspace{-0.2em}\hspace{0.2em}\) と書かずに \(\hspace{-0.2em}\hspace{0.2em}{x_0}^2\hspace{-0.2em}\hspace{0.2em}\) と書くようにしています．あくまで上付き添字ではなく \(\hspace{-0.2em}\hspace{0.2em}(x_0)^2\hspace{-0.2em}\hspace{0.2em}\) ということを強調するためです．一方で上付き添字は \(\hspace{-0.2em}\hspace{0.2em}x^{(2)}\hspace{-0.2em}\hspace{0.2em}\) のようにカッコ付きで書く習慣があります．伝われば何でもいいです．伝わりやすいように心がけているということです．

また，\(\varDelta x^2\hspace{-0.2em}\hspace{0.2em}\) と書かずに \(\hspace{-0.2em}\hspace{0.2em}(\varDelta x)^2\hspace{0.2em}\)と書くようにしています．\(\varDelta(x^2)\hspace{-0.2em}\hspace{0.2em}\) との混同を避けるためです．

文字の定義

何か新しい文字を定義する際には \coloneqq すなわち \(\hspace{-0.2em}\hspace{0.2em}\coloneqq\hspace{-0.2em}\hspace{0.2em}\) を用います．\(\equiv\hspace{-0.2em}\hspace{0.2em}\) を書く人も多いと思いますが，左辺と右辺どちらが定義なのかを強調するために \coloneqq, \eqqcolon を用いるようにしています．:= のように書くと中央が揃わず不適切なのでこれらを用いるようにしましょう．

\cdots と \ldots の使い分け

\cdots と \ldots と使い分けましょう．\(1+2+3+\cdots\hspace{-0.2em}\hspace{0.2em}\) のようなときには \cdots を，\(1,2,3,\ldots\hspace{-0.2em}\hspace{0.2em}\) のようなときには \ldots を使います．

まとめ

今回紹介したのは私の呼吸のほんの一部で，かなり基本的なことだと思います．呼吸であることに気づかないことが多いので，私の資料を見て「これどうやってるの」とかがあれば遠慮なく聞いてください．

場面に合わせて環境などを使い分けると可読性の高いものが仕上がります．（一方で，あまりにこだわりすぎると多分時間が溶けます．）これらに気を配っている学科同期を複数人知っています．幸せな学科ですね．

この記事が多くの PDF の可読性を高めることを期待しています．Happy \(\hspace{-0.2em}\hspace{0.2em}\LaTeX\hspace{-0.2em}\hspace{0.2em}\) ing!