シャボン玉が丸い理由

シャボン玉が丸い理由について，熱力学の言葉も交えて簡単に解説します．

⚠記事の内容は学生個人の見解であり、所属する学科組織を代表するものではありません。

はじめに

理学部１号館の高階層の人聞こえますか〜！

こんにちは．いぇとです．この記事は東京大学理学部物理学科 B3 有志による Physics Lab. 2022 Advent Calendar 2021 25日目の記事です．

Physics Lab. とは物理学科有志による五月祭企画です．私が所属している生物物理班については，たがやし班長が書いてくれた記事『生物物理班だよ』を見てください．

今日はクリスマスですね．皆さんいかがお過ごしですか．私はいまごろ舞浜で上昇と下降を繰り返したりカメと喋ったり骸骨を怒らせたりしていると思います．著作権の関係などで舞浜 × 物理といった記事は書けなさそうです．ちょっぴり残念．

先日，フラクタル構造の話をしたり，夕焼けが赤い理由を説明したり，磁石の話をしたりと，物理のお裾分け（一般向けのお話）をする機会がありまして．そこでの話が楽しかったので，物理にあまり詳しくない人が少しでも楽しめるものを書こうかなという気分になりました．

そこで今回はシャボン玉が丸い理由を説明しようと思います．物理学科で界面の話をきちんと聞いたことはなかったと思うので，物理を多少知っている人向けの説明も後ほどします．

（なおこの記事では脚注をできるだけ付けずにカッコなどを使います．）

物理のお裾分け（クリスマスプレゼント）

まずはざっくりとした説明をします．シャボン玉が丸いことを理解するために，

水の気持ちになる
シャボン玉を見る
シャボン玉の気持ちになる

のステップを踏むことにします．

水の気持ちになる

水には 表面張力 という，表面を縮めようとする力が働いています．この表面張力の仕組みを簡単に考えてみましょう．

水分子同士は水素結合という分子間力によって引きつけあっています．水の内部では，周囲の多数の水分子と引き合って水分子に働く分子間力はつり合っています．一方水の表面では，水分子は内部側からのみ引っ張られます．つまり表面は「不安定」な状態になっています．表面がたくさんあるほど不安定になってしまうので，表面積を小さくしようとする力が働きます．これが表面張力です．

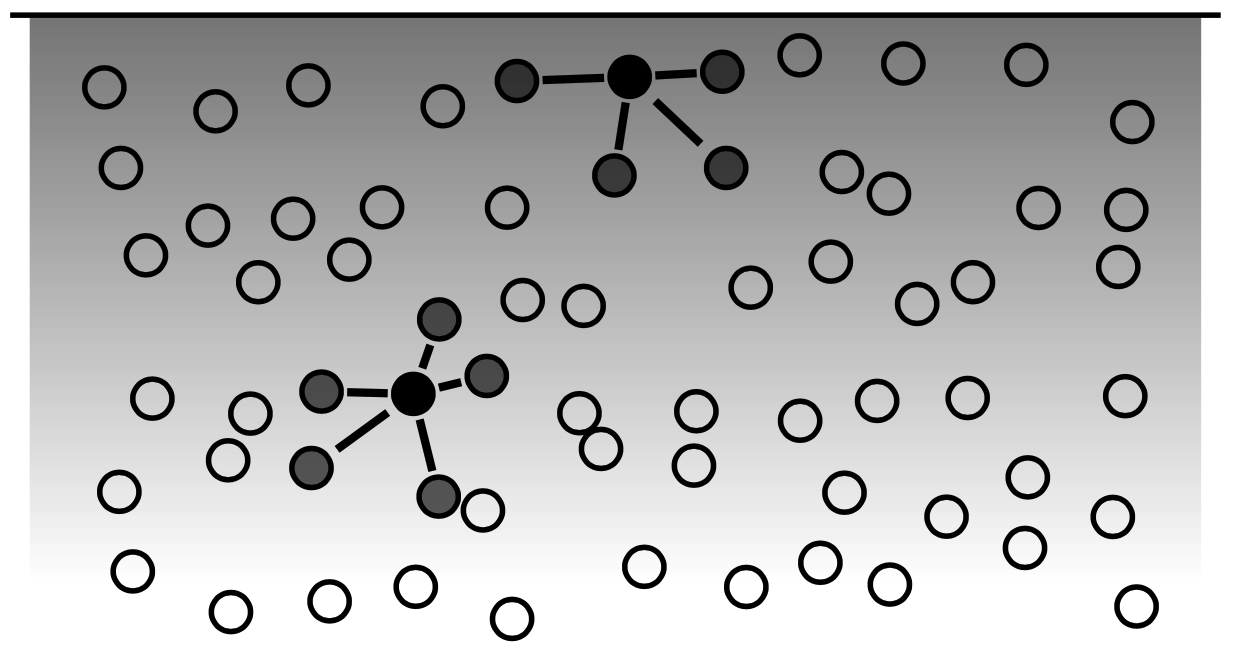
シャボン玉液を使わず水のままでも泡を作ることができるということはわかると思います．しかし，大きな泡を作ることは難しいですし，辛うじてできた泡もすぐに弾けて消えてしまいます．水の表面張力が強すぎるためです．

シャボン玉を見る

実際にシャボン玉を作るときには，洗剤などを使ってシャボン玉液を作ると思います．このシャボン玉の液を 界面活性剤 と言います．界面活性剤の分子は，水に溶けやすい親水基と水に溶けにくい疎水基で構成されています．

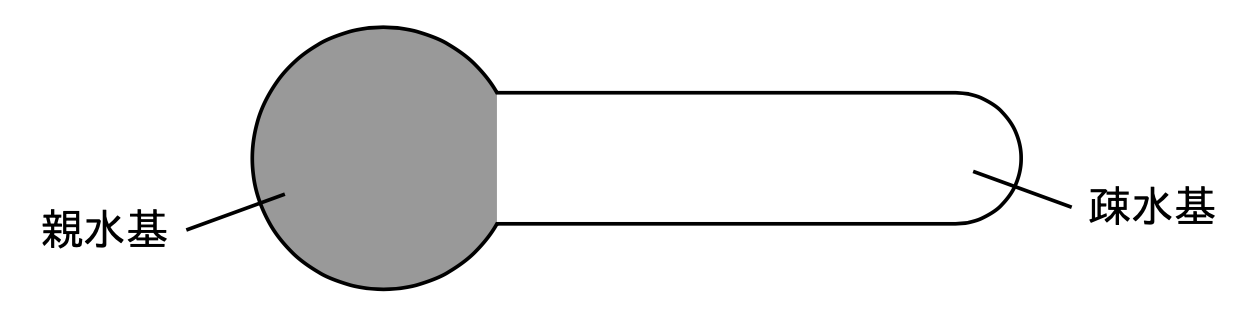
界面活性剤を水に溶かすと，疏水基を持つ構造からわかるように界面活性剤は水の内部では不安定なので，親水基のみが水に溶けたような表面ができます．表面で不安定な水とは違って，界面活性剤は表面で安定です．したがって表面積を縮めようとする作用は弱まり，表面張力が弱くなります．

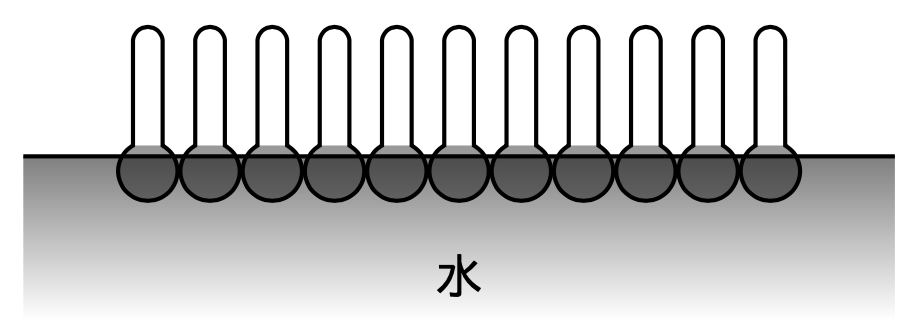
表面張力が弱まるとシャボン玉が作れます．シャボン玉は内部が空洞になっていて，膜が内外を隔てた形になっています．膜の中には親水基が，膜の外には疎水基が飛び出しています．

シャボン玉の気持ちになる

シャボン玉の構造がイメージできたので，実際にシャボン玉の気持ちになってみましょう．

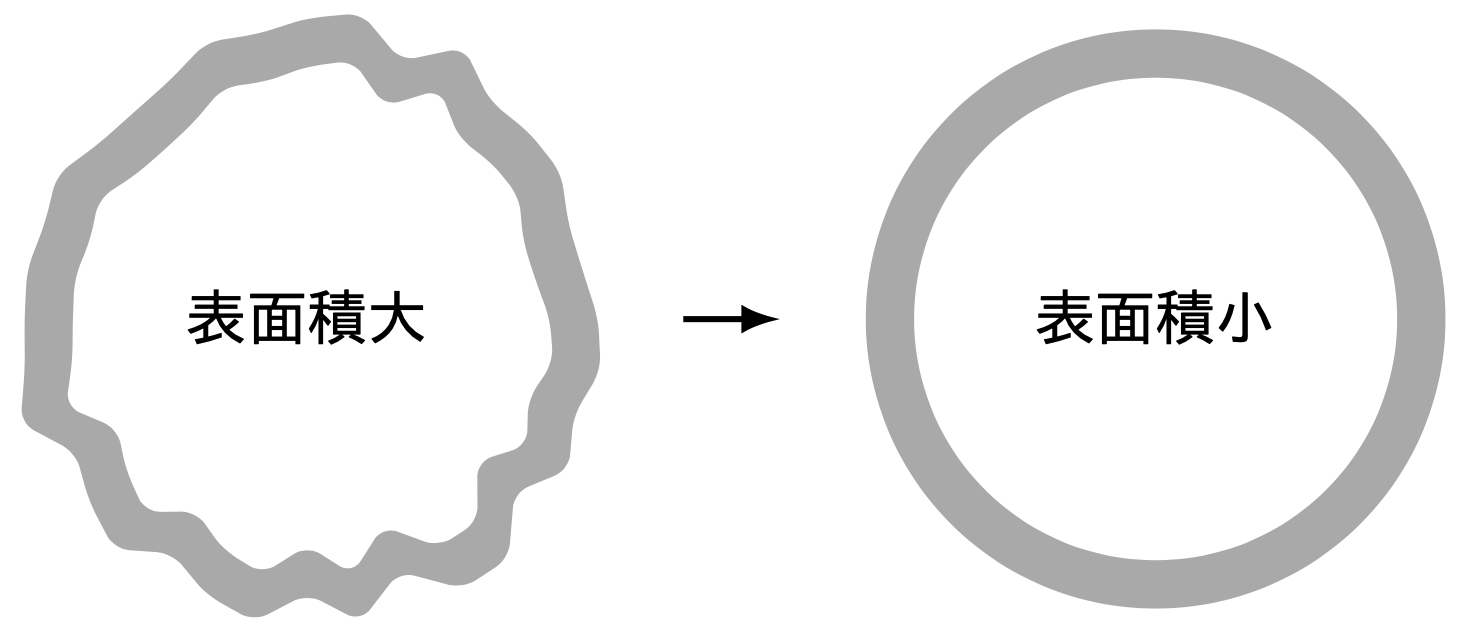
表面張力は弱まりましたが，全くなくなったわけではないです．表面張力とは「表面積を小さくしようとする張力」のことでした．そのことを思い出して，体積を保ちつつ表面積のできるだけ小さな膜を考えると，球形になることがイメージできるでしょうか．たとえば球形ではなく凸凹な形を考えると，表面積がどうしても大きくなってしまうことに気づくでしょう．

したがってシャボン玉は，表面積を最も小さくできる球形になります．逆に「シャボン玉は，表面積を最小にするものが球形であることを教えてくれている」と考えることもできます．頭が上がりません．

表面積を最小にしてくれる他の例

閉じた曲面に対して表面積を最小にするものは球でしたが，他の場合はどうでしょうか．

たとえば，2 つのリングを用意したときのシャボン膜は 懸垂面（catenoid） とよばれる曲面になることが知られています．つまり，この状況では懸垂面が表面積を最小にする曲面であるということです．

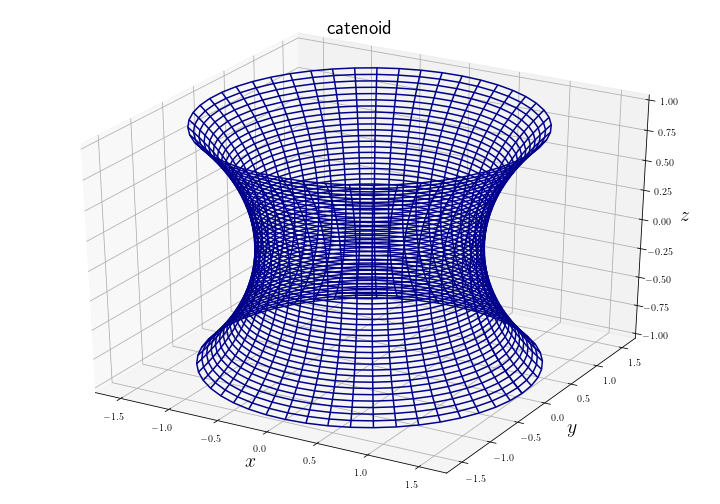
ひもの両端を手で持ったときにひもがたるんでできる曲線が懸垂線になっていることは有名だと思います．実は懸垂面は懸垂線の回転体になっています：

$$ \begin{bmatrix} x\\y\\z \end{bmatrix} =\begin{bmatrix} r\cosh u\cos v\\ r\cosh u\sin v\\ au \end{bmatrix}. $$

他にもいろんなセットアップを用意することでいろんなシャボン膜を考えることができます．シャボン膜は表面積を最小にするという単純な原理に従っていますが，それだけで豊かな数学の問題を与えているようです．

界面の熱力学

ここから先は物理を少し知っている人向けです．いままではシャボン玉を考えてきましたが，もっと一般に界面を考えましょう．

界面張力

界面張力を圧力の類推で導入します．ある閉じた領域の中の流体を考えましょう．流体の圧力 $\hspace{-0.2em}\hspace{0.2em}P\hspace{-0.2em}\hspace{0.2em}$ は，流体の体積を $\hspace{-0.2em}\hspace{0.2em}\varDelta V\hspace{-0.2em}\hspace{0.2em}$ だけ変化させたときの仕事 $\hspace{-0.2em}\hspace{0.2em}W\hspace{-0.2em}\hspace{0.2em}$ を考えて，

$$ W =-P\varDelta V $$

のように定義できます．

同じようにして，界面上に閉じた 2 次元平面を考えます．表面積を $\hspace{-0.2em}\hspace{0.2em}\varDelta A\hspace{-0.2em}\hspace{0.2em}$ だけ変化させたときの仕事を $\hspace{-0.2em}\hspace{0.2em}W\hspace{-0.2em}\hspace{0.2em}$ とすると，界面張力 $\hspace{-0.2em}\hspace{0.2em}\gamma\hspace{-0.2em}\hspace{0.2em}$ は，

$$ W =\gamma \varDelta A $$

のように定義できます．圧力は体積を大きくしようと働く力であるのに対して，界面張力は表面積を小さくしようと働く力であるので，仕事の符号が変わっていることに注意してください．

自由エネルギー

たとえば水と油を考えると，これらは互いに混ざり合いません．混ざり合うことによって不安定になる，すなわちエネルギーが高くなることを意味しています．自由エネルギーを使って記述できそうですね．

セットアップとして，2 つの相 1, 2 が界面を成している状況を考えましょう．相 1, 2 それぞれの自由エネルギーを $\hspace{-0.2em}\hspace{0.2em}J_1,J_2\hspace{-0.2em}\hspace{0.2em}$ とし，界面の自由エネルギーを $\hspace{-0.2em}\hspace{0.2em}J_{12}\hspace{-0.2em}\hspace{0.2em}$ とします．このとき系全体の自由エネルギーは，

$$ J =J_1+J_2+J_{12} $$

と書けます．

平衡状態において 2 つの共存している相の温度を $\hspace{-0.2em}\hspace{0.2em}T\hspace{-0.2em}\hspace{0.2em}$ とします．また，分子種 $\hspace{-0.2em}\hspace{0.2em}i\hspace{-0.2em}\hspace{0.2em}$ の化学ポテンシャルを $\hspace{-0.2em}\hspace{0.2em}\mu^{(i)}\,(i=1,\ldots,m)\hspace{-0.2em}\hspace{0.2em}$ とします．平衡状態を考えているので 2 つの相で $\hspace{-0.2em}\hspace{0.2em}T,\mu^{(i)}\hspace{-0.2em}\hspace{0.2em}$ は同じです．グランドカノニカル分布を考えて，自由エネルギーとしてグランドポテンシャルを採用することにします．グランドポテンシャル $\hspace{-0.2em}\hspace{0.2em}J_1,J_2\hspace{-0.2em}\hspace{0.2em}$ は，それぞれの体積 $\hspace{-0.2em}\hspace{0.2em}V_1,V_2\hspace{-0.2em}\hspace{0.2em}$ を用いて次のように書けます：

$$ \begin{align*} J_1(V_1;T,\mu^{(i)}) &=V_1j_1(T,\mu^{(i)})\\ J_2(V_2;T,\mu^{(i)}) &=V_2j_2(T,\mu^{(i)}). \end{align*} $$

ここで自由エネルギーの示量性を用いました．同様にして，界面のグランドポテンシャル $\hspace{-0.2em}\hspace{0.2em}J_{12}\hspace{-0.2em}\hspace{0.2em}$ は界面の面積 $\hspace{-0.2em}\hspace{0.2em}A\hspace{-0.2em}\hspace{0.2em}$ を用いて次のように書けます：

$$ J_{12}(A;T,\mu^{(i)}) =Aj_{12}(T,\mu^{(i)}). $$

Gibbs-Duhem の式

界面のある場合の Gibbs-Duhem の式を立ててみましょう．グランドポテンシャル $\hspace{-0.2em}\hspace{0.2em}J_1(V_1;T,\mu^{(i)})\hspace{-0.2em}\hspace{0.2em}$ の全微分は，

$$ \mathrm{d}J_1 =-S_1\mathrm{d}T-P_1\mathrm{d}V_1-\sum_{i}^mN_1^{(i)}\mathrm{d}\mu^{(i)} $$

と書けます．$j_1\hspace{-0.2em}\hspace{0.2em}$ を用いた式から，

$$ \mathrm{d}J_1 =V_1\left(\frac{\partial j_1}{\partial T}\mathrm{d}T +\sum_i^m\frac{\partial j_1}{\partial \mu^{(i)}}\mathrm{d}\mu^{(i)}\right) +j_1\mathrm{d}V_1 $$

と書けます．これらの係数を比較することで，

$$ \begin{align*} j_1 &=-P_1,\\ \frac{\partial j_1}{\partial T} &=-\frac{S_1}{V_1},\\ \frac{\partial j_1}{\partial \mu^{(i)}} &=-\frac{N_1^{(i)}}{V_1}\quad(i=1,\ldots,m). \end{align*} $$

と書けます．$j_1=-P_1\hspace{-0.2em}\hspace{0.2em}$ を用いて書き直すと，

$$ \frac{\partial P_1}{\partial T} =\frac{S_1}{V_1},\quad \frac{\partial P_1}{\partial \mu^{(i)}} =\frac{N_1^{(i)}}{V_1}\quad(i=1,\ldots,m). $$

となるので，Gibbs-Duhem の式

$$ V_1\mathrm{d}P_1 =S_1\mathrm{d}T+\sum_i^mN_1^{(i)}\mathrm{d}\mu^{(i)} $$

を得ます．相 2 についても同様に，

$$ V_2\mathrm{d}P_2 =S_2\mathrm{d}T+\sum_i^mN_2^{(i)}\mathrm{d}\mu^{(i)} $$

となります．

界面に対しても同様の議論をしましょう．界面のグランドポテンシャル $\hspace{-0.2em}\hspace{0.2em}J_{12}(A;T,\mu^{(i)})\hspace{-0.2em}\hspace{0.2em}$ は，

$$ \mathrm{d}J_{12} =-S_{12}\mathrm{d}T+\gamma\mathrm{d}A-\sum_i^mN_{12}^{(i)}\mathrm{d}\mu^{(i)}. $$

一方 $\hspace{-0.2em}\hspace{0.2em}J_{12}(A;T,\mu^{(i)})=Aj_{12}(T,\mu^{(i)})\hspace{-0.2em}\hspace{0.2em}$ から，

$$ \mathrm{d}J_{12} =A\left(\frac{\partial j_{12}}{\partial T}\mathrm{d}T +\sum_i^m\frac{\partial j_{12}}{\partial\mu^{(i)}}\mathrm{d}\mu^{(i)}\right) +j_{12}\mathrm{d}A. $$

係数を比較して，

$$ \begin{align*} j_{12} &=\gamma,\\ \frac{\partial j_{12}}{\partial T} &=-\frac{S_{12}}{A},\\ \frac{\partial j_{12}}{\partial \mu^{(i)}} &=-\frac{N_{12}^{(i)}}{A}\quad(i=1,\ldots,m). \end{align*} $$

$\hspace{0.2em}j_{12}=\gamma\hspace{-0.2em}\hspace{0.2em}$ を代入すると，

$$ \frac{\partial\gamma}{\partial T} =-\frac{S_{12}}{A},\quad \frac{\partial\gamma}{\partial \mu^{(i)}} =-\frac{N_{12}^{(i)}}{A}\quad(i=1,\ldots,m). $$

したがって Gibbs-Duhem の式は，

$$ A\mathrm{d}\gamma =-S_{12}\mathrm{d}T-\sum_i^mN_{12}^{(i)}\mathrm{d}\mu^{(i)} $$

となります．

Gibbs の吸着式

界面活性剤のように，液体の界面で安定になる物質を加えると液体の界面張力が下がることを，式の上で簡単に扱ってみましょう．物質 $\hspace{-0.2em}\hspace{0.2em}i=1,\ldots,m\hspace{-0.2em}\hspace{0.2em}$ の中から界面活性剤を選んできて，それを $\hspace{-0.2em}\hspace{0.2em}\text{a}\hspace{-0.2em}\hspace{0.2em}$ と書くことにします．このとき，Gibbs-Duhem の式は，

$$ \frac{\partial \gamma}{\partial \mu_\text{a}} =-\frac{N_{12}^{(\text{a})}}{A} \eqqcolon-\varGamma_\text{a} $$

と書けます．ここで，$\varGamma_\text{a}\coloneqq N_{12}^{(\text{a})}/A\hspace{-0.2em}\hspace{0.2em}$ は単位面積当たりの吸着界面活性剤の数を表し，界面過剰量 といいます．

界面活性剤が増えすぎるとミセルを形成します．ミセルを作らない範囲で界面活性剤濃度が十分小さいとき，化学ポテンシャルは次のように書けます：

$$ \mu_\text{a}(T,n_\text{a}) =\mu_\text{a}^0(T)+k_\text{B}T\log n_\text{a}. $$

このとき，

$$ \frac{\partial \gamma}{\partial n_\text{a}} =\frac{\partial \gamma}{\partial \mu_\text{a}}\frac{\partial\mu_\text{a}}{\partial n_\text{a}} =-k_\text{B}T\frac{\varGamma_\text{a}}{n_\text{a}} $$

と書けます．この式を Gibbs の吸着式 といいます．$\varGamma_\text{a} > 0\hspace{-0.2em}\hspace{0.2em}$ であるような物質（正吸着する物質）を加えると界面張力が下がることが確認できます．

Laplace 圧

自由エネルギーを用いて，シャボン玉の内圧を計算できます．シャボン玉の内側を相 1, 外側を相 2 と呼ぶことにします．シャボン玉の半径を $\hspace{-0.2em}\hspace{0.2em}r\hspace{-0.2em}\hspace{0.2em}$ とし，シャボン玉を含む大きな系の体積を $\hspace{-0.2em}\hspace{0.2em}V\hspace{-0.2em}\hspace{0.2em}$ とします．このとき，

$$ J =\frac{4\pi}{3}r^3j_1+\left(V-\frac{4\pi}{3}r^3\right)j_2+4\pi r^2j_{12} $$

となり，先ほど求めた $\hspace{-0.2em}\hspace{0.2em}j_1=-P_1,j_2=-P_2,j_{12}=\gamma\hspace{-0.2em}\hspace{0.2em}$ の関係式を用いると，

$$ J =-\frac{4\pi}{3}r^3P_1-\left(V-\frac{4\pi}{3}r^3\right)P_2+4\pi r^2\gamma $$

と書けます．平衡状態であるための必要条件は，$\varDelta P\coloneqq P_1-P_2\hspace{-0.2em}\hspace{0.2em}$ とすると，

$$ \frac{\partial J}{\partial r} =-4\pi r^2\varDelta P+8\pi r\gamma =-4\pi r(r\varDelta P-2\gamma) =0 $$

となって，

$$ r=0,\frac{2\gamma}{\varDelta P}. $$

を得ることになります．$r=0\hspace{-0.2em}\hspace{0.2em}$ は物理的な対応がないので，$r=2\gamma/\varDelta P\hspace{-0.2em}\hspace{0.2em}$ がつり合いの位置になります．実はこの点は $\hspace{-0.2em}\hspace{0.2em}J\hspace{-0.2em}\hspace{0.2em}$ の極大を与えていますが，$\varDelta P\hspace{-0.2em}\hspace{0.2em}$ の変化には分子の流出入が必要で，そのような過程はゆっくりです．（膨らんだ風船の口を開けると風船が萎むことに対応しています．そのような分子の流出入はシャボン玉においてかなりゆっくりであると仮定しています．）なお，自由エネルギーを考えずに力のつり合いから求めることもできます．

結局， Laplace 圧 は

$$ \varDelta P =\frac{2\gamma}{r} $$

のように求まります．

等周不等式

「体積一定の閉曲面に対して表面積を最小にするものは球形である」という主張について，ドイツの数学者 Jakob Steiner が考えた方法を概説します．等周不等式の厳密な証明は込み入っているらしい（伝聞）ので，簡単な理解に留めます．

Steiner の対称化

以下，簡単のために 2 次元平面を考えます．

$\hspace{0.2em}C\hspace{-0.2em}\hspace{0.2em}$ を平面内の自己交差を持たない閉曲線とし，$C\hspace{-0.2em}\hspace{0.2em}$ が囲む閉領域を $\hspace{-0.2em}\hspace{0.2em}G\hspace{-0.2em}\hspace{0.2em}$ とする．直線 $\hspace{-0.2em}\hspace{0.2em}l\hspace{-0.2em}\hspace{0.2em}$ に対して，$C\hspace{-0.2em}\hspace{0.2em}$ の Steiner 対称化 $\hspace{-0.2em}\hspace{0.2em}\hat{C}\hspace{-0.2em}\hspace{0.2em}$ は，下の 1., 2. をみたす閉曲線として定義される．

$\hspace{-0.2em}\hspace{0.2em}\hat{C}\hspace{-0.2em}\hspace{0.2em}$ は $\hspace{-0.2em}\hspace{0.2em}l\hspace{-0.2em}\hspace{0.2em}$ について対称である．
$\hspace{-0.2em}\hspace{0.2em}\hat{C}\hspace{-0.2em}\hspace{0.2em}$ が囲む閉領域を $\hspace{-0.2em}\hspace{0.2em}\hat{G}\hspace{-0.2em}\hspace{0.2em}$ とする．$l\hspace{-0.2em}\hspace{0.2em}$ に垂直な任意の直線 $\hspace{-0.2em}\hspace{0.2em}\sigma\hspace{-0.2em}\hspace{0.2em}$ に対し，$\sigma_1\coloneqq\sigma\cap\hat{G}\hspace{-0.2em}\hspace{0.2em}$ は空集合，$l\hspace{-0.2em}\hspace{0.2em}$ 上の 1 点，または次の 2 つをみたす線分である．
- $\hspace{-0.2em}\sigma_1\hspace{-0.2em}\hspace{0.2em}$ は $\hspace{-0.2em}\hspace{0.2em}l\hspace{-0.2em}\hspace{0.2em}$ について対称である．
- $\hspace{-0.2em}\sigma_1\hspace{-0.2em}\hspace{0.2em}$ の長さは $\hspace{-0.2em}\hspace{0.2em}\sigma\cap G\hspace{-0.2em}\hspace{0.2em}$ の長さと一致する．

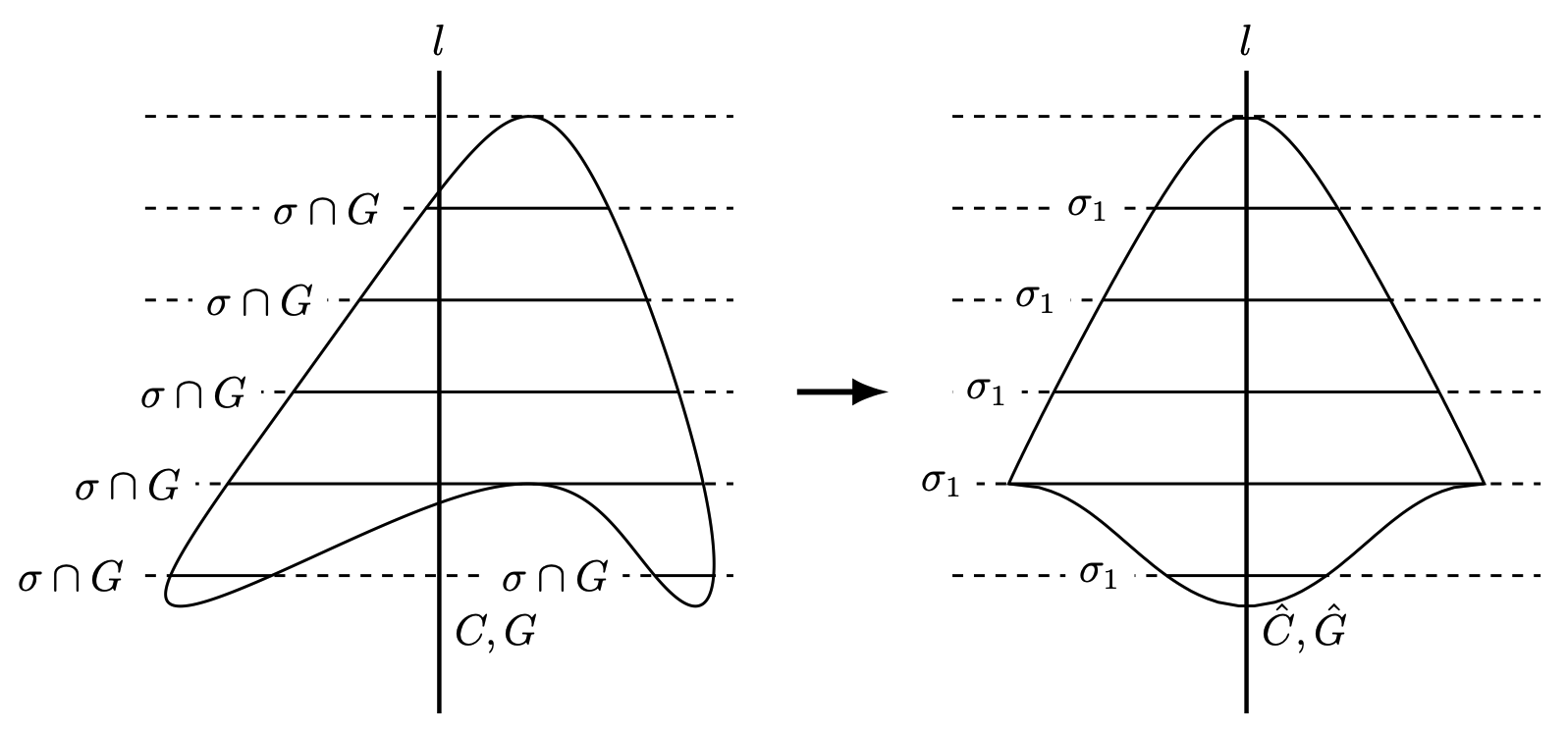
ここで，$G\hspace{-0.2em}\hspace{0.2em}$ の面積を $\hspace{-0.2em}\hspace{0.2em}A(G)$，$C\hspace{-0.2em}\hspace{0.2em}$ の長さを $\hspace{-0.2em}\hspace{0.2em}L(C)\hspace{-0.2em}\hspace{0.2em}$ で表すことにします．このとき，次の [定理 1] が成り立ちます．

[定理 1]

$\hspace{-0.2em}A(G)=A(\hat{G})$．
$\hspace{-0.2em}L(C)\geq L(\hat{C})$．等号は $\hspace{-0.2em}\hspace{0.2em}C\hspace{-0.2em}\hspace{0.2em}$ が $\hspace{-0.2em}\hspace{0.2em}\hat{C}\hspace{-0.2em}\hspace{0.2em}$ の平行移動であるときにのみ成り立つ．

特に $\hspace{-0.2em}\hspace{0.2em}A(G)=A(\hat{G})\hspace{-0.2em}\hspace{0.2em}$ は，$\hat{G}\hspace{-0.2em}\hspace{0.2em}$ の構成からかなり明らかであることがわかると思います．

[定理 1 の証明の概略]

$\hspace{0.2em}l\hspace{-0.2em}\hspace{0.2em}$ 上に $\hspace{-0.2em}\hspace{0.2em}y\hspace{-0.2em}\hspace{0.2em}$ 軸をとるような直交座標系 $\hspace{-0.2em}\hspace{0.2em}(x,y)\hspace{-0.2em}\hspace{0.2em}$ を考えて，直線 $\hspace{-0.2em}\hspace{0.2em}y=y_0\hspace{-0.2em}\hspace{0.2em}$ を $\hspace{-0.2em}\hspace{0.2em}\sigma(y_0)\hspace{-0.2em}\hspace{0.2em}$ と表す．また，$G\hspace{-0.2em}\hspace{0.2em}$ 上の点の $\hspace{-0.2em}\hspace{0.2em}y\hspace{-0.2em}\hspace{0.2em}$ 座標の最大値と最小値をそれぞれ $\hspace{-0.2em}\hspace{0.2em}a,b\hspace{-0.2em}\hspace{0.2em}$ で表す．

$\hspace{0.2em}y\in(a,b)\hspace{-0.2em}\hspace{0.2em}$ に対して，

$$ \sigma(y)\cap\hat{G}=\{(x,y)\mid-\hat{x}(y)\leq x\leq \hat{x}(y)，\hat{x}(y) > 0\} $$

のように $\hspace{-0.2em}\hspace{0.2em}y\hspace{-0.2em}\hspace{0.2em}$ 軸対称に書ける．一方で $\hspace{-0.2em}\hspace{0.2em}\sigma(y)\cap G\hspace{-0.2em}\hspace{0.2em}$ は有限個の線分の和集合として，

\begin{gather*} \sigma(y)\cap G =\bigcup_{i=1}^n I_i,\\ I_i\coloneqq\{(x,y)\mid x_{2i-1}\leq x\leq x_{2i}\},\\ x_1\leq x_2 < x_3\leq x_4 < \cdots < x_{2n-1}\leq x_{2n} \end{gather*}

と書ける．$n,x_i\hspace{-0.2em}\hspace{0.2em}$ は $\hspace{-0.2em}\hspace{0.2em}y\hspace{-0.2em}\hspace{0.2em}$ に依存して決まる．

$\hspace{0.2em}\sigma(y)\cap G\hspace{-0.2em}\hspace{0.2em}$ と $\hspace{-0.2em}\hspace{0.2em}\sigma(y)\cap\hat{G}\hspace{-0.2em}\hspace{0.2em}$ の長さが同じなので，

$$ (x_2-x_1)+(x_4-x_3)+\cdots+(x_{2n}-x_{2n-1}) =2\hat{x}(y). $$

（ここまでで Steiner の対称化を座標を用いて書くことができています．）

$\hspace{0.2em}A(G),A(\hat{G})\hspace{-0.2em}\hspace{0.2em}$ と $\hspace{-0.2em}\hspace{0.2em}L(C),L(\hat{C})\hspace{-0.2em}\hspace{0.2em}$ それぞれの関係を求める．面積については自明で，

$$ A(G) =\int_a^b\sum_{i=1}^{n(y)}\{x_{2i}(y)-x_{2i-1}(y)\}\,\mathrm{d}y =\int_a^b2\hat{x}(y)\,\mathrm{d}y =A(\hat{G}). $$

（曲線が十分滑らかであることを仮定して）長さは，

$$ \begin{align*} L(C) &=\int_a^b\sum_{j=1}^{2n}\sqrt{1+\left(\frac{\mathrm{d}x_j}{\mathrm{d}y}\right)^2}\,\mathrm{d}y,\\ L(\hat{C}) &=2\int_a^b\sqrt{1+\left(\frac{\mathrm{d}\hat{x}}{\mathrm{d}y}\right)^2}\,\mathrm{d}y. \end{align*} $$

ここで，2 次元数ベクトル $\hspace{-0.2em}\hspace{0.2em}\boldsymbol{v}_1,\ldots,\boldsymbol{v}_{2n}\hspace{-0.2em}\hspace{0.2em}$ と $\hspace{-0.2em}\hspace{0.2em}\hat{\boldsymbol{v}}\hspace{-0.2em}\hspace{0.2em}$ を次のように定義する：

$$ \begin{gather*} \boldsymbol{v}_{2i-1} \coloneqq\left(1,-\frac{\mathrm{d}x_{2i-1}}{\mathrm{d}y}\right),\quad \boldsymbol{v}_{2i} \coloneqq\left(1,\frac{\mathrm{d}x_{2i}}{\mathrm{d}y}\right),\\ \hat{\boldsymbol{v}} \coloneqq\sum_{j=1}^{2n}\boldsymbol{v}_j =\left(2n,2\frac{\mathrm{d}\hat{x}}{\mathrm{d}y}\right). \end{gather*} $$

これらを用いて長さを評価すると，途中で三角不等式を用いて，

$$ \begin{align*} L(C) &=\sum_{j=1}^{2n}|\boldsymbol{v}_j|\\ &\geq\left|\sum_{j=1}^{2n}\boldsymbol{v}_j\right| =|\hat{\boldsymbol{v}}| =2\sqrt{n^2+\left(\frac{\mathrm{d}\hat{x}}{\mathrm{d}y}\right)^2}\\ &\geq2\sqrt{1+\left(\frac{\mathrm{d}\hat{x}}{\mathrm{d}y}\right)^2} =L(\hat{C}). \end{align*} $$

等号成立を考える．2 つ目の不等号の等号は $\hspace{-0.2em}\hspace{0.2em}n=1\hspace{-0.2em}\hspace{0.2em}$ のときのみ成り立つ．$n=1\hspace{-0.2em}\hspace{0.2em}$ のときで三角不等式の等号が成り立つことを考えると，必要十分条件は $\hspace{-0.2em}\hspace{0.2em}\boldsymbol{v}_1=\boldsymbol{v}_2\hspace{-0.2em}\hspace{0.2em}$ となる．したがって

$$ -\frac{\mathrm{d}x_{1}}{\mathrm{d}y} =\frac{\mathrm{d}x_2}{\mathrm{d}y} $$

となって，$x_2(y)=-x_1(y)+a\hspace{-0.2em}\hspace{0.2em}$ を得る．これは $\hspace{-0.2em}\hspace{0.2em}x_2(y),x_1(y)\hspace{-0.2em}\hspace{0.2em}$ が $\hspace{-0.2em}\hspace{0.2em}x=a/2\hspace{-0.2em}\hspace{0.2em}$ に関して対称であることを意味している．

等周不等式

[定理 1] を使うと，等周不等式が理解できます．

[2 次元平面における等周不等式]

平面内の閉曲線 $\hspace{-0.2em}\hspace{0.2em}C\hspace{-0.2em}\hspace{0.2em}$ の長さ $\hspace{-0.2em}\hspace{0.2em}L\hspace{-0.2em}\hspace{0.2em}$ と，$C\hspace{-0.2em}\hspace{0.2em}$ が囲む領域 $\hspace{-0.2em}\hspace{0.2em}G\hspace{-0.2em}\hspace{0.2em}$ の面積 $\hspace{-0.2em}\hspace{0.2em}A\hspace{-0.2em}\hspace{0.2em}$ に対して，次の不等式が成り立つ：

$$ L^2 \geq 4\pi A. $$

等号成立は $\hspace{-0.2em}\hspace{0.2em}C\hspace{-0.2em}\hspace{0.2em}$ が円であるときに限る．

この厳密な証明は容易ではないらしい（伝聞）ので避けますが，直感的な理解は容易いです．Steiner の対称化は，閉領域を対称化しながら周長を小さくする操作でした．この操作を何度も何度もいろんな $\hspace{-0.2em}\hspace{0.2em}l\hspace{-0.2em}\hspace{0.2em}$ に対して実行すれば，とても対称な形を構成できて，それが円であることはすぐに理解できます．逆に，円に対してどのような直線 $\hspace{-0.2em}\hspace{0.2em}l\hspace{-0.2em}\hspace{0.2em}$ を持ってきても周長をそれより小さくすることはありません．

円のときが周長最小であることが理解できました．同様のことが 3 次元空間の閉曲面に対しても言うことができます．Steiner の対称化では直線 $\hspace{-0.2em}\hspace{0.2em}l\hspace{-0.2em}\hspace{0.2em}$ に対して垂直な平面を持ってきて，閉領域との交面の面積を一定に保ちながら対称にしていけば良いです．

[3 次元空間における等周不等式]

空間内の閉曲面 $\hspace{-0.2em}\hspace{0.2em}G\hspace{-0.2em}\hspace{0.2em}$ の面積 $\hspace{-0.2em}\hspace{0.2em}S\hspace{-0.2em}\hspace{0.2em}$ と，$G\hspace{-0.2em}\hspace{0.2em}$ が囲む体積 $\hspace{-0.2em}\hspace{0.2em}V\hspace{-0.2em}\hspace{0.2em}$ に対して，次の不等式が成り立つ：

$$ A^3 \ge 36\pi V^2 $$

等号成立は閉曲面 $\hspace{-0.2em}\hspace{0.2em}G\hspace{-0.2em}\hspace{0.2em}$ が球面であるときに限る．

まとめ

この記事の話をまとめましょう：

シャボン玉は表面張力によって表面積最小の球形になる．
界面で安定な界面活性剤によって表面張力が弱まる（Gibbs の吸着式）．
シャボン玉の表面張力によって内圧が外圧よりも少し高くなっている（Laplace 圧）．
表面積最小の閉曲面が球面である（等周不等式）は Steiner の対称化によって理解できる．

結構盛りだくさんになってしまいましたが，学科同期たちが書く記事に比べると簡単な数学や物理しか使っていないと思います．大丈夫大丈夫．

さて，私たちの Advent Calendar もこれにて閉幕です……と思いきや，私たち Physics Lab. 2022 の活動のメインは五月祭の展示です．面白い展示するぞ〜．

参考文献

土井正男『ソフトマター物理学入門』岩波書店 (2010)
小磯深幸『シャボン玉はなぜ丸いか -曲面の変分問題と自然現象-』．九州大学公開講座 (2011)
R. Osserman: The isoperimetric inequality. Bull. Amer. Math. Soc. 84 (1978), no. 6, 1182–1238.
A. E. Treibergs: Inequalities that Imply the Isoperimetric Inequality. Lecture notes (2002).

Twitter	@PhysicsLab_2022
Mail	physlab2022[at]gmail.com