計算機班では、物理現象のコンピュータシミュレーションを展示します。銀河系、空気の流れ、電磁波、分子の運動などを題材に、小さいお子様から物理の専門家まで、見て、触って楽しめるプログラムを用意しております。スーパーコンピュータを使った高速計算も実感していただく予定です。(文・松元 叡一)
五月祭当日に展示したシミュレーションをこちらで公開中!ご利用の環境によっては正常に動作しない場合があります。予めご了承ください。
イントロダクション
シミュレーションとは
科学の研究や工学の製品開発では、何が起こるのかを実物を使って調べるために実験が不可欠です。しかし、「よく飛ぶ飛行機を作りたい」からといって、次々といろんな形の飛行機を作っては飛ばして…を繰り返していては、いくらお金があっても足りません。また、宇宙のように、実験をしたくても規模や距離が大きすぎてどうしようもない研究対象もあります。そこで、私たちは現実世界を単純化して、与えられた資金や時間の範囲内で実験を行います。これが「シミュレーション」です。
 チューリングパターン。生命の体表面の模様にあらわれるパターン。微分方程式で記述できる
チューリングパターン。生命の体表面の模様にあらわれるパターン。微分方程式で記述できる
計算機班では「コンピュータシミュレーション」を展示します。これはその名の通り、コンピュータを使ったシミュレーションです。 コンピュータは数式の計算を非常に高速に行うことができるので、数式で表された世界を再現するのに適しています。 特に、物理学は現実世界を支配する方程式を解明することがひとつの大きな目的ですから、コンピュータシミュレーションとの相性がいいのです。 現在では、生命現象や経済現象のような領域でもコンピュータシミュレーションが適用できるようになってきています。
スーパーコンピュータ
五月祭では、東大が持っているスーパーコンピュータ(略してスパコン)を使った展示も予定しています。 ここで、スパコンを使ったシミュレーションについて少しお話ししましょう。
事業仕分けで話題となったスパコン「京」は1秒間に1京(1億の1億倍)という速さで計算を行うことができます。 これは最近のパソコンの数万倍の速度であり、世界で一番速いコンピュータの座に輝きました。 このとてつもない計算機は、コンピュータシミュレーションのために作られたといっても過言ではありません。
 東大のスーパーコンピュータ「FX10」。京をベースにしている( http://www.cc.u-tokyo.ac.jp/system/fx10/ より転載)
東大のスーパーコンピュータ「FX10」。京をベースにしている( http://www.cc.u-tokyo.ac.jp/system/fx10/ より転載)
 ケルビン・ヘルムホルツ不安定性。密度と速度の違う2流体が接触しているときに界面で現れるパターン。雲や水面波で現れる
ケルビン・ヘルムホルツ不安定性。密度と速度の違う2流体が接触しているときに界面で現れるパターン。雲や水面波で現れる
では、なぜそこまで「速さ」が必要になるのでしょうか? 地球上の大気の動きをシミュレーションをすることを考えてみましょう。これは天気予報や、地球温暖化の予測などに必要になります。 上空数十km程度まで計算することにすると、計算する体積は約1,000京立方メートルになります。この領域を一辺が100mの立方体に区切って、その中では気圧や風速が一定だと考えると、合計で10兆個の立方体があることになります。 そしてこの立方体一つ一つについて1秒後の状態を計算するのに1,000回の計算が必要だとすると、1秒後の地球を計算するために必要な計算回数は1京回。 つまり、スパコン「京」でも1秒間かかってしまうということになります。 この精度で天気予報をするには少し速さが足りませんね。
もちろん明日が晴れか雨か知る程度ならもっと少ない計算で大丈夫でしょうし、実際の気象庁では過去の統計データなども用いて高速に高精度の計算を行なっていると思います。 一方で、台風や竜巻のような現象を再現するには、一辺100mの立方体に区切るというのは粗すぎるでしょう。海流の動きなども考慮するならば、さらに計算量が必要になります。 気象の例以外にも、膨大な計算量が必要な現象はたくさんあります。世界一のコンピュータを目指すのは、こういった理由からなのです。
シミュレーションのご紹介
ここでは私たちが作っているシミュレーションの一部を紹介します。
流体
水や空気のように、流れのある物質のことを一般に「流体」と言います。その運動のシミュレーションは、計算物理学の中でも大きな分野の一つです。 身近な例では飛行機や新幹線の空気抵抗を減らす計算、地球規模では気象シミュレーション、津波のシミュレーション、さらには宇宙のガスなど、本当に様々な適用例があるのが流体の特徴です。コンピュータゲームでの水の表現にも使われています。
 レイリー・テイラー不安定性1。
レイリー・テイラー不安定性1。初期状態。若干中心部が沈降しているが、そのずれは非常に小さい。また、ランダムなゆらぎが与えられている
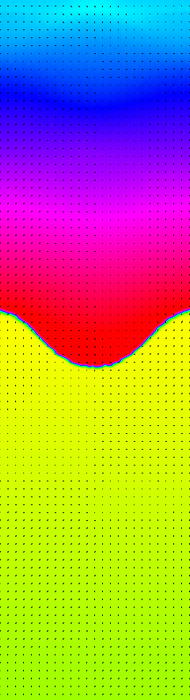 レイリー・テイラー不安定性2。
レイリー・テイラー不安定性2。中間状態。ずれが拡大していっている
 レイリー・テイラー不安定性3。
レイリー・テイラー不安定性3。中間状態。ずれの拡大のなかで各所で同様なずれが生じ、それが拡大する。その過程で自己相似的な模様ができる
 レイリー・テイラー不安定性4。
レイリー・テイラー不安定性4。中間状態。カオス的な様相を見せる
ここにお見せしているのは、2流体の混合の様子です。色が流体の密度を、黒い線が流れを表しています。 初期状態では、上半分が重い流体、下半分が軽い流体となっており、重力に引かれて重い流体が沈みこもうとしています。 しかし、沈み込むには軽い流体を押しのけなければならず、その過程で各所に渦が生じ、拡大していく様子がシミュレーションされています。 このような現象は、水にインクを垂らした時や下降気流などで観察されます。
分子の運動
身の回りのあらゆる物質は「分子」が集まって出来ています。何もないかのように見える空気も、実は無数の窒素分子や水分子が飛び交っています。 分子同士には引きあう力、あるいは反発しあう力がはたらいており、引きあう者同士が集まったら結晶ができたり、分子同士の反発によって熱が伝わったりと、様々な物理的な性質に関与しています。 そこで、物質の中の分子の動きと相互作用をシミュレーションして、物質の性質を調べようというのがここでのテーマです。
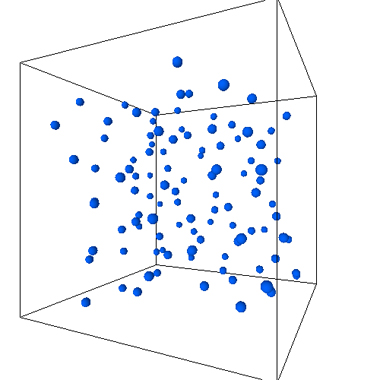 気相。温度が高いと分子はばらばらに運動している。これが気体の状態である
気相。温度が高いと分子はばらばらに運動している。これが気体の状態である
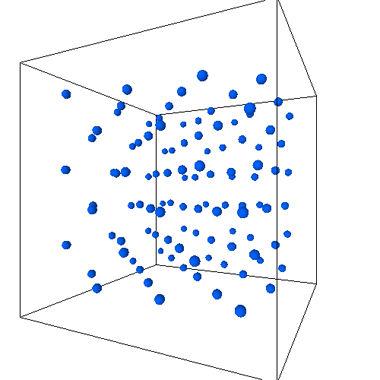 固相。温度を下げると分子は規則的に配列する。これが固体の状態である
固相。温度を下げると分子は規則的に配列する。これが固体の状態である
上の二枚の図は、温度を下げると気体が固体になる凝固の現象をシミュレーションしたものです。 温度が高いと分子は高速で動いているので、分子間に働く力を振りきって自由に運動しています。気体や液体はミクロに見るとこのような状態になっています。 温度を下げると分子同士に働く引力が無視できなくなり、分子同士が集まって規則的に配列します。そこでは分子が持っているエネルギーが低いために分子は束縛された場所から動けません。これが固体の状態になります。
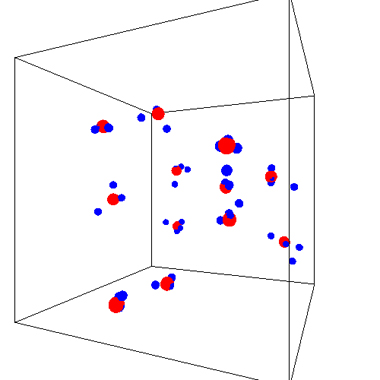 気相。分子はその構造を保っている
気相。分子はその構造を保っている
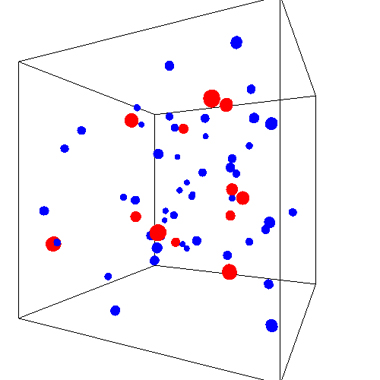 プラズマ。温度を上げると陽イオンと陰イオンが分離してプラズマになる
プラズマ。温度を上げると陽イオンと陰イオンが分離してプラズマになる
この二枚は、気体からプラズマへの変化を表しています。赤い分子と青い分子は電気的な力によって引きあっており、 最初の図ではこれらは結合して複合分子を形成しています。 ここで温度を上げると電気的な力よりも分子の運動エネルギーの方が上回って、結合が切れ、両者が分離した「プラズマ」の状態になります。
カオス
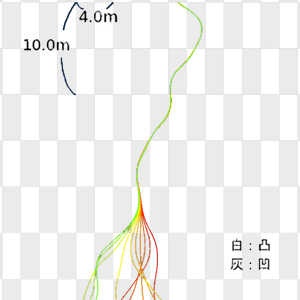 滑り落ちる板のシミュレーション
滑り落ちる板のシミュレーション
物理学における「カオス」とは“全くのランダム”ではなく、一見ランダムではあるが特定の規則に基づいた現象のことを指します。左の画像は、凹凸のついた坂道を板が滑り落ちる様子のシミュレーションです。滑り始める位置を 1cm ずつ横にずらした10枚の板は、始めこそ近い軌跡を辿るものの、坂を 30m も下れば離れていってしまっていることが分かるでしょう。
このようにカオス系では、初めの小さなズレが後の大きな違いを生んでしまいます。身近な例としては天気予報がこの性質を持っています。未来の天候を現在の状態から予測するとき、現在の測定値が少しでもズレていれば、数日後の天気を正しく予報することはできなくなってしまうのです。
フラクタル
私たちの身の回りには、一部分を拡大してもまた同じような構造が続いているようなものがたくさんあります。例えば、木は枝分かれした先にもまた小さい木が続いているように見えますし、海岸線は近くで見ても地図などで大きなスケールで見ても、どちらも同じくらい入り組んだ曲線が見られます。このような、縮尺を変えても構造が変化しない図形のことをフラクタルといいます。
フラクタルはまだ新しい研究分野なので、ある現象がフラクタルかどうかを調べることは出来ても、それがどうしてフラクタルであるのか、また、どうして自然界にはこんなにもフラクタルであふれているのかなど、まだわかっていないこともたくさんあります。
次の画像は、山脈と雲の様子をフラクタルを使ってコンピュータに描かせたものになります。
 フラクタル図形の性質を使って描いた山脈
フラクタル図形の性質を使って描いた山脈
 フラクタル図形の性質を使って描いた雲
フラクタル図形の性質を使って描いた雲
磁石
磁石は切っても砕いても磁石だと言われますが、電子顕微鏡レベルで見ると、それ以上分割できない小さな磁石の集まりだと考えることができます。この小さい磁石は近くにいる他の小磁石と同じ向きを向きたがる性質を持っていて、それによってたくさんの小磁石の向きが揃うことで、磁石全体が磁石としてN極とS極を持つことになるのです。
ところで、小学校か中学校で磁石を火で加熱すると磁石じゃなくなるという実験をやった方もいると思います。なぜ加熱すると磁石じゃなくなってしまうのでしょうか。それは、温度が高いと小磁石の向きが無理やり変えられてしまうことがあるからです。磁石の時は同じ向きに揃っていた小磁石が、熱によって向きを変えられて、全体として磁石じゃなくなってしまうのです。
 低温。磁化している。ところどころ熱ゆらぎでひっくり返っているが、すぐに同じ向きにされる
低温。磁化している。ところどころ熱ゆらぎでひっくり返っているが、すぐに同じ向きにされる
 中温。相転移点である。フラクタル的になっている
中温。相転移点である。フラクタル的になっている
 高温。ランダムな向きを向いていて磁性はなくなっている
高温。ランダムな向きを向いていて磁性はなくなっている
上の図は、このような磁石の温度による状態変化をシミュレーションしたものになります。ここでは小磁石は平面的に並んでいて、赤と青の色がそれぞれ小磁石の「N極が上を向いている状態」、「S極が上を向いている状態」を表しています。1枚目が低温の磁石になっている状態、3枚目が高温の磁石でなくなっている状態、2枚目がその中間の状態です。
さらに深く知りたい人のために
ここでは物理シミュレーションに興味を持った方々を対象に、 中高生でもわかるようにその理論的な背景を解説しました。
物理法則とシミュレーション
コンピュータシミュレーションの出発点は「物理法則」です。 多くの物理法則は「ある量の時間変化が、その量によって決まる」という形をしています。 この形の法則がわかっていれば、その量に関して未来のことが予測できる、つまりシミュレーションができることになります。
たとえば「ある車の位置の時間変化が、その位置によって決まる」としましょう。 位置の時間変化とは速度のことですから、「スタート地点から10メートル地点での速度は毎秒10メートル、10メートル地点から20メートル地点での速度は毎秒20メートル…」といった情報が分かっているということになります。 そうするとこの車は、スタートから0.5秒後には5メートル地点に、1秒後には10メートル地点、1.5秒後には20メートル地点にいるということがわかるでしょう。 つまり、この車の位置について、シミュレーションができたということになります。
コンピュータの仕組み
ここで、コンピュータの仕組みを簡単に説明しておきましょう。 コンピュータの中には計算を行う装置:CPU、記憶を行う装置:メモリ、時計:クロックといった部品が入っています。 メモリには数字や文字などのデータと、CPUが実行するための命令(プログラム)が記録されています。 CPUは、メモリに書かれた命令に従って、メモリ内のデータを使って計算したり、メモリを書きかえたりします。 クロックはオーケストラの指揮者のような動きをしていて、一定時間ごとに信号を発します。CPUなどの部品は、この信号が届いたタイミングで処理を実行します。現代のパソコンではクロックは1秒間に何億回と信号を発するので、それだけの速度でCPUは計算を行なっていることになります。 まとめると、コンピュータは「決められた手順に従って、メモリのデータを計算して書きかえる作業を、1秒間に何億回という高速で行なっている」ということになります。
コンピュータシミュレーション
さて、先程「ある量の時間変化が、その量によって決まる」という物理法則がわかっていれば、シミュレーションができるということを書きました。 これをどうやってコンピュータに計算させるのでしょうか?
ある量を x 、その時間変化を v とします。シミュレーションで知りたいことは、開始地点からある時間 T が経過した時の x の値です。 開始地点で x = 0 のとき、もし v が常に一定ならばその答えは vT となります。秒速 10m で20秒間走り続けたら 10 × 20 = 200m 離れたところにいるということです。
しかしながら、 v は一定では無いので事態はそう単純ではありません。 v は全くの未知というわけではなく、物理法則によって、 x から知ることができます。たとえば「すべての x に対して地点 x での v は 20x である」といった具合です。
では、一気に T 秒後の値を考えずに、ちょっとずつ時間を進めて、その都度 v を求めていけば正しい答えが得られるのではないでしょうか? これがコンピュータシミュレーションの考え方です。
このxについてのシミュレーションは、次の手順で行います。
- (1) メモリに x = 0 と t = 0 を記録する。また、1ステップあたりに進める時間 dt を決めておく。終了時刻を T とする。
- (2) x から v を計算する
- (3) x に v × dt を足す
- (4) t に dt を足す
- (5) t が T に達したら(6)に進む。そうでなければ(2)に戻る
- (6) x を表示して終了
dt が 0.01 、T が 10 ならば、(2)から(5)までは1,000回繰り返されます。 つまり、一気に10秒進めると、 v が一定じゃないことによって誤差が大きくなるけれど、0.01秒ずつ進めれば小さい誤差で済むだろう、ということです。 dt を小さくすればするほど誤差も小さくなりますが、繰り返しの回数が増えるので計算時間もかかってしまいます。
主な活動メンバー
| 松元(4年) | 班長。流体計算の展示を主に作っています。最近物理やらないでプログラミングばかりしているような… |
|---|---|
| 大屋(4年) | カオス系のシミュレーションを作りました。五月祭では他にフィロムジカ交響楽団でビオラを弾いています。 |
| 神山(4年) | 実は五月祭正責任者。気象に関連するシミュレーションを目指しています。 |
| 原田(4年) | 銀河形成や宇宙の大規模構造など、重力で集まってくる物質がどう振る舞うかのシミュレーションをしています。 |
| 荒武(3年) | 拡散方程式(鉄板中の熱伝導)・ラプラス方程式(等電位線・電気力線の描画・翼の周りの気流)・ポアソン方程式(平面上の電荷分布に対する電位)という3つの方程式のシミュレーションを行いました。 |
| 齊藤(3年) | 音楽部管弦楽団でバイオリンを弾いています。5月祭でも演奏会をやってるので、ぜひお越しください。 |
| 新倉(3年) | 新3年生の新倉です。天文が趣味です。計算機初心者ですが、電磁気のシミュレーションに挑戦しました。 |
| 福田(3年) | 計算機班一の情強。GPUを使った並列計算や、量子力学のシミュレーションを作っている。 |
| 室田(3年) | 電磁気のシミュレーションに取り組みました。尊敬できる先輩方と共に五月祭に参加できて嬉しいです。うどん |
| 吉田(3年) | 太陽系みたいなのを作って、自分で惑星を掴んだり投げたりするシミュレーションを作っています。 |
| 矢嶋(3年) | 臨界現象のシュミレーションを作っています。主に丸いものと猫が好きです。 |













