私たちは、比較的新しい学問分野である「経済物理学」のモデルの一つ「PUCK モデル」について勉強し、それに基づいて実際の為替市場を解析しました。 このページでは、その「経済物理学」「PUCK モデル」とは何なのかについて解説します。 五月祭当日の発表では解説に加え、PUCK モデルに基づいた市場価格の未来予測とその結果をアニメーションで見やすく展示する予定です。
物理学は我々の住む世界に何らかの法則が存在すると仮定し、その法則を解き明かしていく学問といえます。
ところで、我々人間が作り出す社会現象の一つとして、金融市場において行われる経済活動があります。 経済物理学は、物理学の試みと同じように、人間が作ったこの金融市場などの経済現象に「基本原理」「基本方程式」が存在すると仮定し、これらの原理を探求していく新しい学問です。
さて、探求のためには金融市場をうまく説明するような数式モデルを作ることが重要になります。
従来の経済学では金融市場のモデルとして、投げたコインの表裏に応じて価格の上がり下がりが変化するという「ランダムウォークモデル」が挙げられていました。

図1 : ランダムウォークのイメージ
この「ランダムウォークモデル」は長い時間尺度で見ると実際の金融市場を再現しますが、短い時間スケールでは現実の金融市場と矛盾することがあります。
具体的には、主に、
の2 つの状態がランダムウォークと異なります。
経済物理学では、このような困難に対抗するため、物理学の手法を用いて経済の問題に取り組みます。
今回私たちは、そのモデルの一つである「PUCK(Potential of Unbalanced Complex Kinetics)モデル」を用いた発表を行います。
「PUCK モデル」とは、価格を粒子のようなものとみたときにその粒子が動く原因として力が加わっていると考えることができるように、 何らかの力を市場のモデルにも組み込んで、その力で価格の変動を説明するという、東工大の高安先生が考案したモデルです。 このモデルの説明に入る前に、これからしばしば使う言葉を定義します。
金融市場のデータ解析には、通常の意味での時間(物理時間)のほかに、ティック時間と呼ばれる時間も用いられます。 これは、取引価格が更新されるたびに時間を1 進めるというものです。 物理時間と異なり実際のディーラーたちの活動時間、取引量のムラに影響を受けずに解析を行うことができるという点で優れています。 ティック時間に基づいた市場価格のデータをティックデータと呼びます。今回の解析でもこのティックデータを用いました。
\(n\)ティック目の価格を\(X(n)\)と表すことにします。 この価格が比較的近い過去に比べてどのくらい高いのか、または低いのかを評価するために、過去\(M\)ティックまで遡った平均値を\(X_M(n)\)と定義します。 式で表すと、 \begin{eqnarray*} X_M(n) &=& \frac{1}{M}\sum^{M-1}_{k=0} X(n-k)\\ &=& \frac{1}{M}[X(n)+X(n-1)+\cdots+X(n-(M-1))] \end{eqnarray*} です。 実際の市場を解析してみると、
の2者には多くの場合、比例関係があるようです(\(M\)の値は市場によって異なります。目安としては、私たちは\(M=5\)を使いました)。 ただしその比例係数は、同じ市場でもしばしば(ニュースなどが入ると)変わり、さらに正の場合も負の場合もあります。
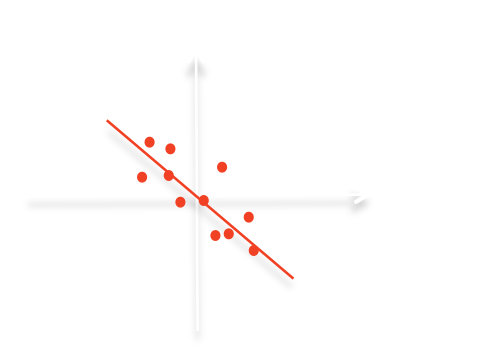

図2 : 1と2の関係の例です。それぞれで比例係数の符号が違います。
この現象をふまえてPUCK モデルでは、価格には、\(X(n)-X_M(n)\)の値に比例した”ばね”のような力がはたらいて、次の価格に影響を及ぼすと仮定します。
ただし、通常のばねとは異なり、ばね定数が負の値になることもあります。
式で表すと、
\[
X(n+1)-X(n) = -\frac{b_2(n)}{M-1}\left[X(n)-X_M(n)\right]+G(n)
\]
となります。ここで、\(-\frac{b_2(n)}{M-1}\)が力の比例係数で、\(G(n)\)はランダム項(確率的に決まる変数)です。
上の図から分かるように完全に比例するわけではないので、このようなランダム項を入れる必要があります。
式の意味は、\(n+1\) ティック目の価格は、\(n\)ティック目の価格に力による変位を加えて、さらにランダム項を加えたものだということです。
この状況で力を全く考えないものが、先述のランダムウォークです。
ランダム項を含むため、完璧な予測はできませんが、ランダムウォークモデルよりは方向性をもった予測ができます。
\(b_2(n)\)は市場の現在の状態を表す重要なパラメーターです。
この値が正のときは、価格が乖離すると逆の方向に力がはたらくので、価格変動はある一つの価格の周りで多少ばらつくだけの安定なものになります。
逆に負のときは、価格が変動した向きと同じ向きに力がはたらくので、価格変動は同じ方向に続けて起こりやすい不安定なものになります。
基本的に\(b_2(n)\)の値はあまり変動しませんが、突然のニュースなどが市場に影響を与えると、正から負になったり、逆に負から正になったりします。


図3 : \(b_2(n)\)が正のときの安定な市場(左)と、そのときの力のイメージ(右)です。


図4 : \(b_2(n)\)が負のときの不安定な市場(左)と、そのときの力のイメージ(右)です。
図 3,4 の右の図のように、粒子がどこにあるときにどのように力がはたらくかというのを高さで表現したものを、「ポテンシャル」といいます。
つまり、ポテンシャルの勾配が急であるほど大きな力がはたらくということです。PUCK の P は、このポテンシャルのことです。
実は、暴落や暴騰のときなどには、"ばね"のような\(X(n)-X_M(n)\)の値に比例する力とは違う形の力(つまり、図 3,4 とは違う形のポテンシャル)が観測されるようです。この状況における研究もされていますが、我々は比例する場合をメインテーマとして扱います。
私たちはこのPUCK モデルを使って、為替相場の未来予想ができるのか挑戦します。
用いるデータはTrueFX(http://www.truefx.com)から入手した為替相場です。
このサイトでは、簡単にアカウントを作れて、主要な通貨の過去のティックデータを無料で閲覧することができます。
(追記:取引頻度が高すぎるようなので、時間の単位としてティックではなく秒を用いることにしました)
具体的には、まず、それぞれのティック時刻から1000ティック程度まで過去に遡り、図 2(下に再掲)のように直線をフィットさせて、\(b_2(n)\)の値を推定します。


図2 の再掲
次に、その\(b_2(n)\)の値が続くと考えて、ランダム項としてコンピュータで発生させた乱数を用い、未来の価格がどうなるかという計算を10000回程度行います。 この計算によって、どの程度の確率で価格がどのようになっていくかという予想を立てます。 具体的に言うと、70%の確率で価格がいくらになっていくかを下の図のように表示します。 このように、コンピュータで乱数を発生させて行う実験を「モンテカルロ・シミュレーション」と言います。

図5 : 価格の予想のイメージ
五月祭当日には、為替相場の予想値と実際の値の比較をアニメーションで見やすく展示する予定です。是非いらしてください!!
市場では、売り値と買い値が交互に更新されやすく、そのように売り手と買い手が押し合う結果として、 それぞれの価格が1 ティック刻みで見るとギザギザになることがあるようです。 このような場合は、数学的な方法を用いて、より滑らかな「最適移動平均価格」というものを計算します。 そして、この最適移動平均価格をPUCK モデルに適用します。

図6 : 実際の価格と、そこから計算した最適移動平均価格の例
今回私たちが解析したデータでは、このギザギザな特徴は見られなかったので、この操作は行いませんでした。 最適移動平均の計算の話はやや数学的にややこしいのでここでは割愛します(参考文献に上げた「計算と社会」に載っています)。